
科目: 来源: 题型:
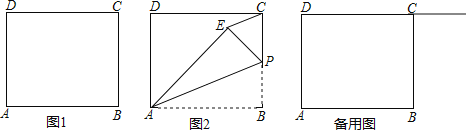
【题目】问题情境:在综合与实践课上,同学们以“已知三角形三边的长度,求三角形面积”为主题开展数学活动,小颖想到借助正方形网格解决问题。图1、图2都是8×8的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点。
操作发现:小颖在图1中画出△ABC,其顶点A、B、C都是格点,同时构造正方形BDEF,使它的顶点都在格点上,且它的边DE、EF分别经过点C、A,她借助此图求出了△ABC的面积。
(1)在图1中,小颖所画的△ABC的三边长分别是AB= ,BC= ,AC= ;△ABC的面积为 。
(2)请你根据小颖的思路,在图2中以格点为顶点画一个△DEF,使三角形三边长分别为2、![]() 、
、![]() ,并直接写出△DEF的面积= 。
,并直接写出△DEF的面积= 。

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点P是等边三角形ABC内一点,且PA=3,PB=4,PC=5,若将△APB绕着点B逆时针旋转后得到△CQB。

(1)△BPQ是 三角形;
(2)求PQ的长度;
(3)求∠APB的度数。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,BA=BC,BD是三角形的角平分线,DE∥BC交AB于E,下列结论:①∠1=∠3;②![]() ;③
;③![]() 。正确的有__________。(填序号)
。正确的有__________。(填序号)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过A(-1,0)、B(4,0)、C(0,2)三点.
(1)求该二次函数的解析式;
(2)点D是该二次函数图象上的一点,且满足∠DBA=∠CAO(O是坐标原点),求点D的坐标;
(3)点P是该二次函数图象上位于一象限上的一动点,连接PA分别交BC,y轴与点E、F,若△PEB、△CEF的面积分别为S1、S2,求S1-S2的最大值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G.
(1)求证:DF∥AO;
(2)若AC=6,AB=10,求CG的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知四边形ABCD中,AB=10cm,BC=8cm,CD=12cm,∠B=∠C,点E为AB的中点.如果点P在线段BC上以3cm/s的速度沿B-C-B运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为_______cm/s时,能够使△BPE≌△CQP.

查看答案和解析>>
科目: 来源: 题型:
【题目】一次函数y=kx+b(k≠0)的图象经过点A(2,-6),且与反比例函数y=-![]() 的图象交于点B(a,4)
的图象交于点B(a,4)
(1)求一次函数的解析式;
(2)将直线AB向上平移10个单位后得到直线l:y1=k1x+b1(k1≠0),l与反比例函数y2= ![]() 的图象相交,求使y1<y2成立的x的取值范围.
的图象相交,求使y1<y2成立的x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在四边形ABCD中,![]() ,
,![]() ,
,![]() .
.
![]() 为边BC上一点,将
为边BC上一点,将![]() 沿直线AP翻折至
沿直线AP翻折至![]() 的位置
的位置![]() 点B落在点E处
点B落在点E处![]()
![]() 如图1,当点E落在CD边上时,利用尺规作图,在图1中作出满足条件的图形
如图1,当点E落在CD边上时,利用尺规作图,在图1中作出满足条件的图形![]() 不写作法,保留作图痕迹,用2B铅笔加粗加黑
不写作法,保留作图痕迹,用2B铅笔加粗加黑![]() 并直接写出此时
并直接写出此时![]() ______;
______;
![]() 如图2,若点P为BC边的中点,连接CE,则CE与AP有何位置关系?请说明理由;
如图2,若点P为BC边的中点,连接CE,则CE与AP有何位置关系?请说明理由;
![]() 点Q为射线DC上的一个动点,将
点Q为射线DC上的一个动点,将![]() 沿AQ翻折,点D恰好落在直线BQ上的点
沿AQ翻折,点D恰好落在直线BQ上的点![]() 处,则
处,则![]() ______;
______;
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com