
科目: 来源: 题型:
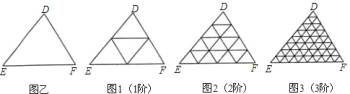
【题目】一般地,“任意三角形都是自相似图形”,只要顺次连接三角形各边中点,则可将原三角形分割为四个都与它自己相似的小三角形.我们把![]() (图乙)第一次顺次连接各边中点所进行的分割,称为
(图乙)第一次顺次连接各边中点所进行的分割,称为![]() 阶分割(如图
阶分割(如图![]() );把
);把![]() 阶分割得出的
阶分割得出的![]() 个三角形再分别顺次连接它的各边中点所进行的分割,称为
个三角形再分别顺次连接它的各边中点所进行的分割,称为![]() 阶分割(如图
阶分割(如图![]() )…,依此规则操作下去.
)…,依此规则操作下去.![]() 阶分割后得到的每一个小三角形都是全等三角形(
阶分割后得到的每一个小三角形都是全等三角形(![]() 为正整数),设此时小三角形的面积为
为正整数),设此时小三角形的面积为![]() .请写出一个反映
.请写出一个反映![]() ,
,![]() ,
,![]() 之间关系的等式________.
之间关系的等式________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=x2-2x-3的图象与x轴交于A,B两点,与y轴交于点C,连接BC,点D为抛物线的顶点,点P是第四象限的抛物线上的一个动点(不与点D重合).
(1)求∠OBC的度数;
(2)连接CD,BD,DP,延长DP交x轴正半轴于点E,且S△OCE=S四边形OCDB,求此时P点的坐标;
(3)过点P作PF⊥x轴交BC于点F,求线段PF长度的最大值.

查看答案和解析>>
科目: 来源: 题型:
【题目】(10分)已知∠MAN=135°,正方形ABCD绕点A旋转.
(1)当正方形ABCD旋转到∠MAN的外部(顶点A除外)时,AM,AN分别与正方形ABCD的边CB,CD的延长线交于点M,N,连接MN.
①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是 ;
②如图2,若BM≠DN,请判断①中的数量关系是否仍成立?若成立,请给予证明;若不成立,请说明理由;
(2)如图3,当正方形ABCD旋转到∠MAN的内部(顶点A除外)时,AM,AN分别与直线BD交于点M,N,探究:以线段BM,MN,DN的长度为三边长的三角形是何种三角形,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】观察下表:
序号 | 1 | 2 | 3 | … |
图形 | x x | |||
y | ||||
x x | x x x | |||
y y | ||||
x x x | ||||
y y | ||||
x x x | x x x x | |||
y y y | ||||
x x x x | ||||
y y y | ||||
x x x x | ||||
y y y | ||||
x x x x | … |
我们把某格中字母的和所得到的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y.回答下列问题:
(1)第2格的“特征多项式”为____,第n格的“特征多项式”为____;(n为正整数)
(2)若第1格的“特征多项式”的值为-8,第2格的“特征多项式”的值为-11.
①求x,y的值;
②在此条件下,第n格的“特征多项式”是否有最小值?若有,求最小值和相应的n值;若没有,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(9分)如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若A的对应点A2的坐标为(0,4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知正方形ABCD的边长为6,E,F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.

(1)求证:EF=MF;
(2)若AE=2,求FC的长.
查看答案和解析>>
科目: 来源: 题型:
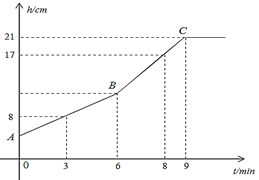
【题目】某兴趣小组观察下雨天学校池塘水面高度h(单位:cm)与观察时间t(单位:min)的关系,并根据当天观察数据画出了如图所示的图象,请你结合图象回答下列问题:
(1)求线段BC的表达式;
(2)试求出池塘原有水面的高度.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中有点A(0,0),点A第1次运动到点A1(0,1),第2次运动到点A2(1,0),第3次运动到点A3(1,1),第4次运动到点A4(0,0),第5次运动到点A5(![]() ,1),第6次运动到点A6(
,1),第6次运动到点A6(![]() ,0),第7次运动到点A7(0,1),第8次运动到点A8(0,2),第9次运动到点A9(1,1)…,依次规律运动下去,点A第2019次运动到点A2019的坐标是( )
,0),第7次运动到点A7(0,1),第8次运动到点A8(0,2),第9次运动到点A9(1,1)…,依次规律运动下去,点A第2019次运动到点A2019的坐标是( )
A.(1,288)B.(0,288)C.(1,289)D.(0,289)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com