
科目: 来源: 题型:
【题目】如图1,⊿ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向⊿ABC作等腰Rt⊿ABE和等腰Rt⊿ACF,过点E、F作射线GA的垂线,垂足分别为P、Q。
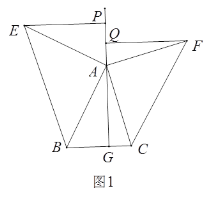
(1)求证:⊿AEP≌⊿BAG;
(2)试探究EP与FQ之间的数量关系,并证明你的结论;
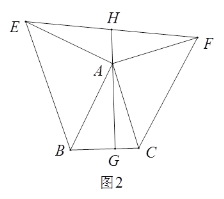
(3)如图2,若连接EF交GA的延长线于H,由(2)中的结论你能判断EH与FH的大小关系吗?并说明理由;
(4)在(3)的条件下,若BC=AG=10,请直接写出S⊿AEF= .
查看答案和解析>>
科目: 来源: 题型:
【题目】△ABC是一块直角三角形纸片,∠ACB=90°,将该三角形纸片折叠,使点A与点C重合,DE为折痕.
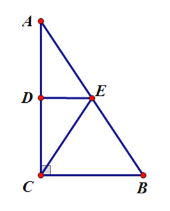
(1)线段AE和BE有怎样的数量关系?写出你的结论并进行证明.
结论: .
证明:
(2)直角三角形斜边的中线和斜边有怎样的数量关系?写出你的结论(不证明).
结论: .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,ABCO的顶点A,B的坐标分别是A(3,0),B(0,2),动点P在直线y=![]() x上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与四边形ABCO的边所在直线相切时,P点的坐标为_____.
x上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与四边形ABCO的边所在直线相切时,P点的坐标为_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正三角形![]() 的边长为
的边长为![]() .
.
![]() 如图①,正方形
如图①,正方形![]() 的顶点
的顶点![]() 、
、![]() 在边
在边![]() 上,顶点
上,顶点![]() 在边
在边![]() 上,在正三角形
上,在正三角形![]() 及其内部,以点
及其内部,以点![]() 为位似中心,作正方形
为位似中心,作正方形![]() 的位似正方形
的位似正方形![]() ,且使正方形
,且使正方形![]() 的面积最大(不要求写作法);
的面积最大(不要求写作法);
![]() 求
求![]() 中作出的正方形
中作出的正方形![]() 的边长;
的边长;
![]() 如图②,在正三角形
如图②,在正三角形![]() 中放入正方形
中放入正方形![]() 和正方形
和正方形![]() ,使得
,使得![]() 、
、![]() 在边
在边![]() 上,点
上,点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,求这两个正方形面积和的最大值和最小值,并说明理由.
上,求这两个正方形面积和的最大值和最小值,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,IB,IC分别平分∠ABC,∠ACB,过I点作DE∥BC,分别交AB于D,交AC于E,给出下列结论:①△DBI是等腰三角形;②△ACI是等腰三角形;③AI平分∠BAC;④△ADE周长等于AB+AC,其中正确的是: ___________(只需填写序号)。
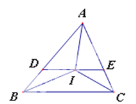
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,D是边长为4㎝的等边△ABC的边AB上的一点,DQ⊥AB交边BC于点Q,RQ⊥BC交边AC于点R,RP⊥AC交边AB于点E,交QD的延长线于点P.


图1 图2
①请说明△PQR是等边三角形的理由;
②若BD=1.3㎝,则AE=_______㎝(填空)
③如图2,当点E恰好与点D重合时,求出BD的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:![]() 在直角坐标平面内,三个顶点的坐标分别为
在直角坐标平面内,三个顶点的坐标分别为![]() 、
、![]() 、
、![]() (正方形网格中每个小正方形的边长是一个单位长度).
(正方形网格中每个小正方形的边长是一个单位长度).

![]() 向下平移
向下平移![]() 个单位长度得到的
个单位长度得到的![]() ,点
,点![]() 的坐标是________;
的坐标是________;
![]() 以点
以点![]() 为位似中心,在网格内画出
为位似中心,在网格内画出![]() ,使
,使![]() 与
与![]() 位似,且位似比为
位似,且位似比为![]() ,点
,点![]() 的坐标是________;(画出图形)
的坐标是________;(画出图形)
![]() 的面积是________平方单位.
的面积是________平方单位.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.
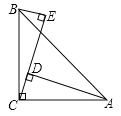
(1)直线BE与AD的位置关系是 ;BE与AD之间的距离是线段 的长;
(2) 若AD=6cm,BE=2cm.,求BE与AD之间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com