
科目: 来源: 题型:
【题目】满足下列条件的三角形中,不是直角三角形的是( )
A.∠A-∠B=∠CB.∠A:∠B:∠C=3: 4: 7
C.∠A=2∠B=3∠CD.∠A=9°,∠B=81°
查看答案和解析>>
科目: 来源: 题型:
【题目】综合与实践
问题情境
在学习了《勾股定理》和《实数》后,某班同学以“已知三角形三边的长度,求三角形面积”为主题开展了数学活动.
操作发现
“毕达哥拉斯”小组的同学想到借助正方形网格解决问题.如图1是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点.在图1中画出△ABC,其顶点A,B,C都是格点,同时构造正方形BDEF,使它的顶点都在格点上,且它的边DE,EF分别经过点C、A,他们借助此图求出了△ABC的面积.

(1)在图1中,所画的△ABC的三边长分别是AB= ,BC= ,AC= ; △ABC的面积为 .
实践探究
(2)在图2所示的正方形网格中画出△DEF(顶点都在格点上),使DE=![]() ,DF=
,DF=![]() , EF=
, EF=![]() ,并写出△DEF的面积.
,并写出△DEF的面积.
继续探究
“秦九韶”小组的同学想到借助曾经阅读的数学资料: 已知三角形的三边长分别为a、b、c,求其面积,对此问题中外数学家曾经进行过深入研究.古希腊的几何学家海伦(Heron,约公元50年),在他的著作《度量》一书中,给出了求其面积的海伦公式:
![]()
我国南宋时期数学家秦九韶(约1202 ~1261),给出了著名的秦九韶公式:

(3)一个三角形的三边长依次为![]() ,
,![]() ,
,![]() ,请你从上述材料中选用适当的公式 求这个三角形的面积.(写出计算过程)
,请你从上述材料中选用适当的公式 求这个三角形的面积.(写出计算过程)
查看答案和解析>>
科目: 来源: 题型:
【题目】国家推行“节能减排,低碳经济”政策后,某企业推出一种叫“CNG”的改烧汽油为天然气的装置,每辆车改装费为b元,如图所示l1和l2分别表示每辆车的燃料费(含改装费)y(元)与正常运营时间x(天)之间的关系.

(1)哪条线表示每辆车改装后的燃料费(含改装费)y(元)与正常运营时间x(天)之间的关系?
(2)每辆车的改装费b= 元,正常营运 天后,就可以从节省的燃料费中收回改装成本;
(3)每辆车改装前每天的燃料费为 元;改装后每天的燃料费为 元;
(4)直接写出每辆车改装前、后的燃料费(含改装费)y(元)与正常运营时间x(天)之间的关系式.
查看答案和解析>>
科目: 来源: 题型:
【题目】在一次蜡烛燃烧实验中,蜡烛燃烧时剩余部分的高度y(cm)是燃烧时间x(h) 的一次函数.某蜡烛的高度为30cm,燃烧3h后,蜡烛剩余部分的高度为12cm.
(1)求蜡烛燃烧时y(cm)与x(h)之间的函数表达式;
(2)求出蜡烛从点燃到燃尽所用的时间.
查看答案和解析>>
科目: 来源: 题型:
【题目】为庆祝祖国70华诞,某小区计划在一块面积为196m2的正方形空地上建一个面积为100m2的长方形花坛(长方形的边与正方形空地的边平行),要求长方形的长是宽的2倍.请你通过计算说明该小区能否实现这个愿望?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线![]() 与
与![]() 交于A,B两点,且点A的横坐标为4,过原点O的另一条直线l交双曲线
交于A,B两点,且点A的横坐标为4,过原点O的另一条直线l交双曲线![]() 于P,Q两点(点P在第一象限),由点A,B,P,Q为顶点组成的四边形面积为24,则点P的坐标为_________.
于P,Q两点(点P在第一象限),由点A,B,P,Q为顶点组成的四边形面积为24,则点P的坐标为_________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,分别以长方形OABC的边OC,OA所在直线为x轴、y轴,建立平面直角坐 标系.已知AO=13,AB=5,点E在线段OC上,以直线AE为轴,把△OAE翻折,点O的对应点D恰好落在线段BC上.则点E的坐标为_______.
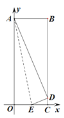
查看答案和解析>>
科目: 来源: 题型:
【题目】已知在△ABC中,AB=AC在射线AC上取一点D,以D为顶点、DB为一条边作∠BDF=∠A,点E在AC的延长线上,∠ECF=∠ACB
(1)如图(1),当点D在边AC上时,求证:①∠FDC=∠ABD②DB=DF
(2)如图(2),当点D在AC的延长线上时,请判断DB与DF是否相等,并说明理由

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,点D是边BC的中点,CE∥AB,AD平分∠EAB
(1)延长AD、CE相交于点F,求证:AB=CE+AE
(2)当点E和点C重合时,试判断△ABC的形状,请画出图形,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com