
科目: 来源: 题型:
【题目】某校八年级全体同学参加了“爱心一日捐捐款活动,该校随杋抽査了部分同学捐款的情况统计如图所示:

(1)求出本次抽查的学生人数;
(2)求出捐款10元的学生人数,并将条形图补充完整;
(3)捐款金额的众数是 元,中位数是 .
(4)请估计全校八年级1000名学生,捐款20元的有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】七年级某班为准备科技节表彰的奖品,计划从友谊超市购买笔记本和水笔共40件,在获知某网店有“五一”促销活动后,决定从该网店购买这些奖品.已知笔记本和水笔在这两家商店的零售价分别如下表,且在友谊超市购买这些奖品需花费90元.
品名商店 | 笔记本(元/件) | 水笔(元/件) |
友谊超市 | 2.4 | 2 |
网店 | 2 | 1.8 |
(1)请求出需购买笔记本和水笔的数量;
(2)求从网店购买这些奖品可节省多少元.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,连接在一起的两个等边三角形的边长都为1cm,一个微型机器人由点A开始按A→B→C→D→E→C→A→B→C…的顺序沿等边三角形的边循环移动.当微型机器人移动了2019cm后,它停在了点_____上.
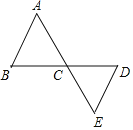
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)探索发现:如图1,已知Rt△ABC中,∠ACB=90°,AC=BC,直线l过点C,过点A作AD⊥l,过点B作BE⊥l,垂足分别为D、E.求证:AD=CE,CD=BE.
(2)迁移应用:如图2,将一块等腰直角的三角板MON放在平面直角坐标系内,三角板的一个锐角的顶点与坐标原点O重合,另两个顶点均落在第一象限内,已知点M的坐标为(1,3),求点N的坐标.
(3)拓展应用:如图3,在平面直角坐标系内,已知直线y=﹣3x+3与y轴交于点P,与x轴交于点Q,将直线PQ绕P点沿逆时针方向旋转45°后,所得的直线交x轴于点R.求点R的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,l1和l2分别是走私船和我公安快艇航行路程与时间的函数图象,请结合图象解决下列问题:
(1)在刚出发时,我公安快艇距走私船多少海里?
(2)计算走私船与公安艇的速度分别是多少?
(3)求出l1,l2的解析式.
(4)问6分钟时,走私船与我公安快艇相距多少海里?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,CP平分∠ACB,其中正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】在等边三角形ABC中,点D是BC的中点,点E、F分别是边AB、AC(含线段AB、AC的端点)上的动点,且∠EDF=120°,小明和小慧对这个图形展开如下研究:
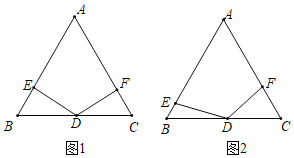
问题初探:(1)如图1,小明发现:当∠DEB=90°时,BE+CF=nAB,则n的值为 ;
问题再探:(2)如图2,在点E、F的运动过程中,小慧发现两个有趣的结论:
①DE始终等于DF;②BE与CF的和始终不变;请你选择其中一个结论加以证明.
成果运用:(3)若边长AB=8,在点E、F的运动过程中,记四边形DEAF的周长为L,L=DE+EA+AF+FD,则周长L 取最大值和最小值时E点的位置?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(―3,6)、B(―9,一3),以原点O为位似中心,相似比为![]() ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )

A.(―1,2)
B.(―9,18)
C.(―9,18)或(9,―18)
D.(―1,2)或(1,―2)
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:如果经过三角形一个顶点的线段把这个三角形分成两个小三角形,其中一个三角形是等腰三角形,另外一个三角形和原三角形的三个内角分别相等,那么这条线段称为原三角形的“和谐分割线”,例如:如图1,等腰直角三角形斜边上的中线就是一条“和谐分割线”
![]() 判断下列两个命题是真命题还是假命题
判断下列两个命题是真命题还是假命题![]() 填“真”或“假”
填“真”或“假”![]()
![]() 等边三角形必存在“和谐分割线”
等边三角形必存在“和谐分割线”
![]() 如果三角形中有一个角是另一个角的两倍,则这个三角形必存在“和谐分割线”.
如果三角形中有一个角是另一个角的两倍,则这个三角形必存在“和谐分割线”.
命题![]() 是______命题,命题
是______命题,命题![]() 是______命题;
是______命题;
![]() 如图2,
如图2,![]() ,
,![]() ,
,![]() ,
,![]() ,试探索
,试探索![]() 是否存在“和谐分割线”?若存在,求出“和谐分割线”的长度;若不存在,请说明理由.
是否存在“和谐分割线”?若存在,求出“和谐分割线”的长度;若不存在,请说明理由.
![]() 如图3,
如图3,![]() 中,
中,![]() ,若线段CD是
,若线段CD是![]() 的“和谐分割线”,且
的“和谐分割线”,且![]() 是等腰三角形,求出所有符合条件的
是等腰三角形,求出所有符合条件的![]() 的度数.
的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com