
科目: 来源: 题型:
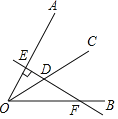
【题目】已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D作直线DE⊥OA,垂足为点E,且直线DE交OB于点F,如图所示,若DE=1,则DF=_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H,交BE于G.下列结论:①BD=CD;②AD+CF=BD;③CE=![]() BF;④AE=BG.其中正确的是
BF;④AE=BG.其中正确的是

A. ①② B. ①③ C. ①②③ D. ①②③④
查看答案和解析>>
科目: 来源: 题型:
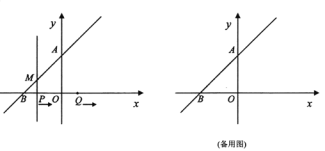
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() 的面积为2,动点
的面积为2,动点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度在射线
出发,以每秒1个单位长度的速度在射线![]() 上运动,动点
上运动,动点![]() 从
从![]() 出发,沿
出发,沿![]() 轴的正半轴与点
轴的正半轴与点![]() 同时以相同的速度运动,过
同时以相同的速度运动,过![]() 作
作![]() 轴交直线
轴交直线![]() 于
于![]() .
.
(1)求直线![]() 的解析式.
的解析式.
(2)当点![]() 在线段
在线段![]() 上运动时,设
上运动时,设![]() 的面积为
的面积为![]() ,点
,点![]() 运动的时间为
运动的时间为![]() 秒,求
秒,求![]() 与
与![]() 的函数关系式(直接写出自变量的取值范围).
的函数关系式(直接写出自变量的取值范围).
(3)过点![]() 作
作![]() 轴交直线
轴交直线![]() 于
于![]() ,在运动过程中(点
,在运动过程中(点![]() 不与点
不与点![]() 重合),是否存在某一时刻
重合),是否存在某一时刻![]() (秒),使
(秒),使![]() 是等腰三角形?若存在,求出时间
是等腰三角形?若存在,求出时间![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】初二![]() 班同学从学校出发去某自然保护区研学旅行,一部分乘坐大客车先出发,余下的几人20分钟后乘坐小轿车沿同一路线出行
班同学从学校出发去某自然保护区研学旅行,一部分乘坐大客车先出发,余下的几人20分钟后乘坐小轿车沿同一路线出行![]() 大客车中途停车等候,小轿车赶上来之后,大客车以出发时速度的
大客车中途停车等候,小轿车赶上来之后,大客车以出发时速度的![]() 继续行驶,小轿车保持原速度不变
继续行驶,小轿车保持原速度不变![]() 小轿车司机因路线不熟错过了景点入口,再原路提速返回,恰好与大客车同时到达景点入口
小轿车司机因路线不熟错过了景点入口,再原路提速返回,恰好与大客车同时到达景点入口![]() 两车距学校的路程
两车距学校的路程![]() 单位:千米
单位:千米![]() 和行驶时间
和行驶时间![]() 单位:分钟
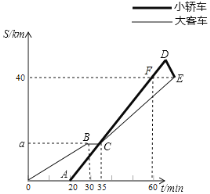
单位:分钟![]() 之间的函数关系如图所示.
之间的函数关系如图所示.
请结合图象解决下面问题:
![]() 学校到景点的路程为______千米,大客车途中停留了______分钟,
学校到景点的路程为______千米,大客车途中停留了______分钟,![]() ______千米;
______千米;
![]() 在小轿车司机驶过景点入口时,大客车离景点入口还有多远?
在小轿车司机驶过景点入口时,大客车离景点入口还有多远?
![]() 若大客车一直以出发时的速度行驶,中途不再停车,那么小轿车折返后到达景点入口,需等待______分钟,大客车才能到达景点入口.
若大客车一直以出发时的速度行驶,中途不再停车,那么小轿车折返后到达景点入口,需等待______分钟,大客车才能到达景点入口.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:如图1,在平面直角坐标系中,点M是二次函数![]() 图象上一点,过点M作
图象上一点,过点M作![]() 轴,如果二次函数
轴,如果二次函数![]() 的图象与
的图象与![]() 关于l成轴对称,则称
关于l成轴对称,则称![]() 是
是![]() 关于点M的伴随函数
关于点M的伴随函数![]() 如图2,在平面直角坐标系中,二次函数
如图2,在平面直角坐标系中,二次函数![]() 的函数表达式是
的函数表达式是![]() ,点M是二次函数
,点M是二次函数![]() 图象上一点,且点M的横坐标为m,二次函数
图象上一点,且点M的横坐标为m,二次函数![]() 是
是![]() 关于点M的伴随函数.
关于点M的伴随函数.



![]() 若
若![]() ,
,
![]() 求
求![]() 的函数表达式.
的函数表达式.
![]() 点
点![]() ,
,![]() 在二次函数
在二次函数![]() 的图象上,若
的图象上,若![]() ,a的取值范围为______.
,a的取值范围为______.
![]() 过点M作
过点M作![]() 轴,
轴,
![]() 如果
如果![]() ,线段MN与
,线段MN与![]() 的图象交于点P,且MP:
的图象交于点P,且MP:![]() :3,求m的值.
:3,求m的值.
![]() 如图3,二次函数
如图3,二次函数![]() 的图象在MN上方的部分记为
的图象在MN上方的部分记为![]() ,剩余的部分沿MN翻折得到
,剩余的部分沿MN翻折得到![]() ,由
,由![]() 和
和![]() 所组成的图象记为
所组成的图象记为![]() .以
.以![]() 、
、![]() 为顶点在x轴上方作正方形
为顶点在x轴上方作正方形![]() 直接写出正方形ABCD与G有三个公共点时m的取值范围.
直接写出正方形ABCD与G有三个公共点时m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】我们知道,任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果mx+n=0,其中m、n为有理数,x为无理数,那么m=0且n=0.
(1)如果![]() ,其中a、b为有理数,那么a= ,b= .
,其中a、b为有理数,那么a= ,b= .
(2)如果![]() ,其中a、b为有理数,求a+2b的值.
,其中a、b为有理数,求a+2b的值.
查看答案和解析>>
科目: 来源: 题型:
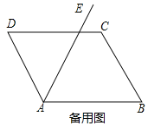
【题目】如图1,在□ABCD中,![]() ,
,![]() ,
,![]() ,射线AE平分
,射线AE平分![]() 动点P以
动点P以![]() 的速度沿AD向终点D运动,过点P作
的速度沿AD向终点D运动,过点P作![]() 交AE于点Q,过点P作
交AE于点Q,过点P作![]() ,过点Q作
,过点Q作![]() ,交PM于点
,交PM于点![]() 设点P的运动时间为
设点P的运动时间为![]() ,四边形APMQ与四边形ABCD重叠部分面积为
,四边形APMQ与四边形ABCD重叠部分面积为![]()


![]() ______
______![]() 用含t的代数式表示
用含t的代数式表示![]()
![]() 当点M落在CD上时,求t的值.
当点M落在CD上时,求t的值.
![]() 求S与t之间的函数关系式.
求S与t之间的函数关系式.
![]() 如图2,连结AM,交PQ于点G,连结AC、BD交于点H,直接写出t为何值时,GH与三角形ABD的一边平行或共线.
如图2,连结AM,交PQ于点G,连结AC、BD交于点H,直接写出t为何值时,GH与三角形ABD的一边平行或共线.
查看答案和解析>>
科目: 来源: 题型:
【题目】感知:如图1,在![]() 中,D、E分别是AB、AC两边的中点,延长DE至点F,使
中,D、E分别是AB、AC两边的中点,延长DE至点F,使![]() ,连结
,连结![]() 易知
易知![]() ≌
≌![]() .
.



探究:如图2,AD是![]() 的中线,BE交AC于点E,交AD于点F,且
的中线,BE交AC于点E,交AD于点F,且![]() ,求证:
,求证:![]() .
.
应用:如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,DE是
,DE是![]() 的中位线
的中位线![]() 过点D、E作
过点D、E作![]() ,分别交边BC于点F、G,过点A作
,分别交边BC于点F、G,过点A作![]() ,分别与FD、GE的延长线交于点M、N,则四边形MFGN周长C的取值范围是______.
,分别与FD、GE的延长线交于点M、N,则四边形MFGN周长C的取值范围是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com