
【题目】定义:如图1,在平面直角坐标系中,点M是二次函数![]() 图象上一点,过点M作
图象上一点,过点M作![]() 轴,如果二次函数
轴,如果二次函数![]() 的图象与
的图象与![]() 关于l成轴对称,则称
关于l成轴对称,则称![]() 是
是![]() 关于点M的伴随函数
关于点M的伴随函数![]() 如图2,在平面直角坐标系中,二次函数
如图2,在平面直角坐标系中,二次函数![]() 的函数表达式是
的函数表达式是![]() ,点M是二次函数
,点M是二次函数![]() 图象上一点,且点M的横坐标为m,二次函数
图象上一点,且点M的横坐标为m,二次函数![]() 是
是![]() 关于点M的伴随函数.
关于点M的伴随函数.



![]() 若
若![]() ,
,
![]() 求
求![]() 的函数表达式.
的函数表达式.
![]() 点
点![]() ,
,![]() 在二次函数
在二次函数![]() 的图象上,若
的图象上,若![]() ,a的取值范围为______.
,a的取值范围为______.
![]() 过点M作
过点M作![]() 轴,
轴,
![]() 如果
如果![]() ,线段MN与
,线段MN与![]() 的图象交于点P,且MP:
的图象交于点P,且MP:![]() :3,求m的值.
:3,求m的值.
![]() 如图3,二次函数
如图3,二次函数![]() 的图象在MN上方的部分记为
的图象在MN上方的部分记为![]() ,剩余的部分沿MN翻折得到
,剩余的部分沿MN翻折得到![]() ,由
,由![]() 和
和![]() 所组成的图象记为
所组成的图象记为![]() .以
.以![]() 、
、![]() 为顶点在x轴上方作正方形
为顶点在x轴上方作正方形![]() 直接写出正方形ABCD与G有三个公共点时m的取值范围.
直接写出正方形ABCD与G有三个公共点时m的取值范围.
【答案】![]()
![]() 的函数表达式为
的函数表达式为![]() ,
, ![]()
![]() ;
;
![]() 或
或![]() ,
, ![]() 当
当![]() 或
或![]() 时,G与正方形ABCD有三个公共点.
时,G与正方形ABCD有三个公共点.
【解析】
![]() 根据题意,当
根据题意,当![]() 时,可得到抛物线
时,可得到抛物线![]() 的顶点为
的顶点为![]() ,再用顶点式写出函数表达式即可;
,再用顶点式写出函数表达式即可;
![]() 由点
由点![]() ,
,![]() 在二次函数
在二次函数![]() 的图象上,得到
的图象上,得到![]() ,再根据
,再根据![]() ,可得a的取值范围;
,可得a的取值范围;
![]() 由
由![]() 轴,MP:
轴,MP:![]() :3,得到
:3,得到![]() ,然后根据当m>0和m<0时,分情况讨论即可得到答案;
,然后根据当m>0和m<0时,分情况讨论即可得到答案;
![]() 通过分别分析当m=
通过分别分析当m=![]() ,1,
,1,![]() ,2值,得到正方形与G的公共点数,从而得到正方形与G有三个公共点时m的取值范围.
,2值,得到正方形与G的公共点数,从而得到正方形与G有三个公共点时m的取值范围.
![]() 当
当![]() 时,抛物线
时,抛物线![]() 与抛物线
与抛物线![]() 关于直线
关于直线![]() 对称,
对称,
![]() 抛物线
抛物线![]() 的顶点是
的顶点是![]() ,
,
![]() 抛物线
抛物线![]() 的解析式为
的解析式为![]() ;
;
![]() 点
点![]() ,
,![]() 在二次函数
在二次函数![]() 的图象上,
的图象上,
∴![]() ,
,
当![]() 时,
时,![]() ,
,
解得:![]() ,
,
故答案为:![]() ;
;
![]() 轴,MP:
轴,MP:![]() :3,
:3,
∴![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
故![]() 或
或![]() ;
;
![]() 分析图象可知:
分析图象可知:
当![]() 时,可知C1和G的对称轴关于直线
时,可知C1和G的对称轴关于直线![]() 对称,
对称,![]() 的顶点恰在AD上,此时G与正方形有2个公共点,
的顶点恰在AD上,此时G与正方形有2个公共点,
当![]() 时,G与正方形ABCD有三个公共点,
时,G与正方形ABCD有三个公共点,
当![]() 时,直线MN与x轴重合,G与正方形有三个公共点,
时,直线MN与x轴重合,G与正方形有三个公共点,
当1<m<![]() 时,G与正方形ABCD有五个公共点,
时,G与正方形ABCD有五个公共点,
当m=![]() 时,G的顶点与点C(3,2)重合,且G对称轴左侧部分与正方形有三个公共点,
时,G的顶点与点C(3,2)重合,且G对称轴左侧部分与正方形有三个公共点,
当![]() <m<2时,G与正方形ABCD有四个个公共点,
<m<2时,G与正方形ABCD有四个个公共点,
当![]() 时,G过点
时,G过点![]() 且G对称轴左侧部分与正方形有两个公共点,
且G对称轴左侧部分与正方形有两个公共点,
故当![]() 或
或![]() 时,G与正方形ABCD有三个公共点.
时,G与正方形ABCD有三个公共点.


科目:初中数学 来源: 题型:
【题目】放置在水平桌面上的台灯的灯臂AB长为40 cm,灯罩BC长为30 cm,底座厚度为2 cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少厘米?(结果精确到0.1 cm,参考数据:![]() ≈1.732)
≈1.732)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点![]() 的直线
的直线![]() 与一次函数
与一次函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
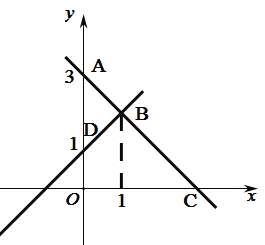
(1)求![]() 的坐标及直线
的坐标及直线![]() 的函数表达式;
的函数表达式;
(2)求直线![]() 与
与![]() 轴的交点
轴的交点![]() 的坐标;
的坐标;
(3)![]() 为
为![]() 的图象与
的图象与![]() 轴的交点,求四边形
轴的交点,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:如图1,在![]() 中,D、E分别是AB、AC两边的中点,延长DE至点F,使
中,D、E分别是AB、AC两边的中点,延长DE至点F,使![]() ,连结
,连结![]() 易知
易知![]() ≌
≌![]() .
.



探究:如图2,AD是![]() 的中线,BE交AC于点E,交AD于点F,且
的中线,BE交AC于点E,交AD于点F,且![]() ,求证:
,求证:![]() .
.
应用:如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,DE是
,DE是![]() 的中位线
的中位线![]() 过点D、E作
过点D、E作![]() ,分别交边BC于点F、G,过点A作
,分别交边BC于点F、G,过点A作![]() ,分别与FD、GE的延长线交于点M、N,则四边形MFGN周长C的取值范围是______.
,分别与FD、GE的延长线交于点M、N,则四边形MFGN周长C的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 在
在![]() 的正北方向,
的正北方向,![]() 在
在![]() 的正东方向,且
的正东方向,且![]() .某一时刻,甲车从
.某一时刻,甲车从![]() 出发,以
出发,以![]() 的速度朝正东方向行驶,与此同时,乙车从
的速度朝正东方向行驶,与此同时,乙车从![]() 出发,以
出发,以![]() 的速度朝正北方向行驶.
的速度朝正北方向行驶.![]() 小时后,位于点
小时后,位于点![]() 处的观察员发现甲、乙两车之间的夹角为
处的观察员发现甲、乙两车之间的夹角为![]() ,即
,即![]() ,此时,甲、乙两人相距的距离为( )
,此时,甲、乙两人相距的距离为( )

A. 90km B. 50![]() km C. 20
km C. 20![]() km D. 100km
km D. 100km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() ,
,![]() ,
,![]()
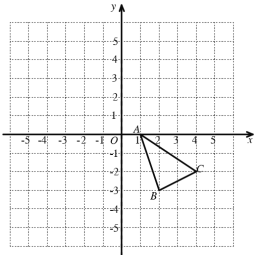
(1)画出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ,画出
,画出![]() 向左平移3个单位长度后得到的
向左平移3个单位长度后得到的![]() ,
,
(2)如果![]() 上有一点
上有一点![]() 经过上述两次变换,那么对应
经过上述两次变换,那么对应![]() 上的点
上的点![]() 的坐标是______
的坐标是______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 过点
过点![]() 和
和![]() 对于该二次函数有如下说法:
对于该二次函数有如下说法:
①它的图象与![]() 轴有两个公共点;
轴有两个公共点;
②若存在一个正数![]() ,使得当
,使得当![]() 时,函数值
时,函数值![]() 随
随![]() 的增大而减小,则
的增大而减小,则![]() ;若存在一个负数
;若存在一个负数![]() ,使得当
,使得当![]() 时,函数值
时,函数值![]() 随
随![]() 的增大而增大,则
的增大而增大,则![]() ;
;
③若将它的图象向左平移![]() 个单位后过原点,则
个单位后过原点,则![]() ;
;
④若当![]() 时的函数值与
时的函数值与![]() 时的函数值相等,则当
时的函数值相等,则当![]() 时的函数值为
时的函数值为![]() .
.
其中正确的说法的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com