
科目: 来源: 题型:
【题目】如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“奇巧数”,如![]() ,
,![]() ,
,![]() ,,因此
,,因此![]() ,
,![]() ,
,![]() 都是奇巧数.
都是奇巧数.
(1)![]() ,
,![]() 是奇巧数吗?为什么?
是奇巧数吗?为什么?
(2)设两个连续偶数为![]() ,
,![]() (其中
(其中![]() 为正整数),由这两个连续偶数构造的奇巧数是4的倍数吗?为什么?
为正整数),由这两个连续偶数构造的奇巧数是4的倍数吗?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)填写下表,观察被开方数![]() 的小数点与算术平方根
的小数点与算术平方根![]() 的小数点的移动规律:
的小数点的移动规律:
| 0.0016 | 0.16 | 16 | 1600 |
| 0.04 | 0.4 |
(2)根据你发现的规律填空:
①已知![]() ,则
,则![]() .
.
②已知![]() ,
,![]() ,则
,则![]() 是
是![]() 的 倍.
的 倍.
查看答案和解析>>
科目: 来源: 题型:
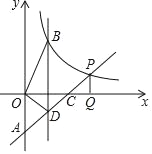
【题目】直线y=x﹣2与两坐标轴分别交于点A,C,交y=![]() (x>0)于点P,PQ⊥x轴于点Q,CQ=1.
(x>0)于点P,PQ⊥x轴于点Q,CQ=1.
(1)求反比例函数解析式;
(2)平行于y轴的直线x=m分别交y=x﹣2,y=![]() (x>0)于点D,B(B在线段AP上方),若S△BOD=2,求m值.
(x>0)于点D,B(B在线段AP上方),若S△BOD=2,求m值.
查看答案和解析>>
科目: 来源: 题型:
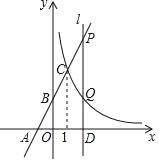
【题目】如图,直线y=kx+2与x轴,y轴分别交于点A(﹣1,0)和点B,与反比例函数y=![]() 的图象在第一象限内交于点C(1,n).
的图象在第一象限内交于点C(1,n).
(1)求一次函数y=kx+2与反比例函数y=![]() 的表达式;
的表达式;
(2)过x轴上的点D(a,0)作平行于y轴的直线l(a>1),分别与直线y=kx+2和双曲线y=![]() 交于P、Q两点,且PQ=2QD,求点D的坐标.
交于P、Q两点,且PQ=2QD,求点D的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,面积为4的正方形OABC的顶点O与坐标原点重合,边OA、OC分别在x轴、y轴的正半轴上,点B、P都在函数y=![]() (x>0)的图象上,过动点P分别作轴x、y轴的平行线,交y轴、x轴于点D、E.设矩形PDOE与正方形OABC重叠部分图形的面积为S,点P的横坐标为m.
(x>0)的图象上,过动点P分别作轴x、y轴的平行线,交y轴、x轴于点D、E.设矩形PDOE与正方形OABC重叠部分图形的面积为S,点P的横坐标为m.
(1)求k的值;
(2)用含m的代数式表示CD的长;
(3)求S与m之间的函数关系式.

查看答案和解析>>
科目: 来源: 题型:
【题目】下列从左边到右边的变形,是因式分解的是( )
A.y![]() ﹣5y﹣6=(y﹣6)(y+1)B.a
﹣5y﹣6=(y﹣6)(y+1)B.a![]() +4a﹣3=a(a+4)﹣3
+4a﹣3=a(a+4)﹣3
C.x(x﹣1)=x![]() ﹣xD.m
﹣xD.m![]() +n
+n![]() =(m+n)(m﹣n)
=(m+n)(m﹣n)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=![]() 的图象相交于A(﹣2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+
的图象相交于A(﹣2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+![]() n=0;③S△AOP=S△BOQ;④不等式k1x+b>
n=0;③S△AOP=S△BOQ;④不等式k1x+b>![]() 的解集是x<﹣2或0<x<1,其中正确的结论的序号是_____.
的解集是x<﹣2或0<x<1,其中正确的结论的序号是_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】问题:(1)如图①,在Rt△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC,则线段BC,DC,EC之间满足的等量关系式为 ;
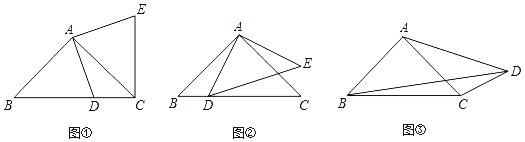
探索:(2)如图②,在Rt△ABC与Rt△ADE中,AB=AC,AD=AE,将△ADE绕点A旋转,使点D落在BC边上,试探索线段AD,BD,CD之间满足的等量关系,并证明你的结论;
应用:(3)如图③,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°.若BD=9,CD=3,求AD的长.
查看答案和解析>>
科目: 来源: 题型:
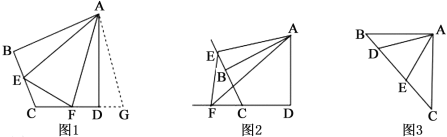
【题目】如图1,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,点E,F分别在四边形ABCD的边BC,CD上,∠EAF=![]() ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系.
∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系.
(1)思路梳理
将△ABE绕点A逆时针旋转至△ADG,使AB与AD重合,由∠B+∠ADC=180°,得∠FDG=180°,即点F,D,G三点共线,易证△AFG≌△AFE,故EF,BE,DF之间的数量关系为__;
(2)类比引申
如图2,在图1的条件下,若点E,F由原来的位置分别变到四边形ABCD的边CB,DC延长线上,∠EAF=![]() ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°,若BD=1,EC=2,直接写出DE的长为________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com