
科目: 来源: 题型:
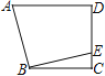
【题目】如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD=8,过点B作EB⊥AB,交CD于点E.若DE=6,则AD的长为___________.
查看答案和解析>>
科目: 来源: 题型:
【题目】在一个不透明的布袋中装有三个小球,小球上分别标有数字-2、l、2,它们除了数字不同外,其它都完全相同.
(1)随机地从布袋中摸出一个小球,则摸出的球为标有数字l的小球的概率为 .
(2)小红先从布袋中随机摸出一个小球,记下数字作为![]() 的值,再把此球放回袋中搅匀,由小亮从布袋中随机摸出一个小球,记下数字作为
的值,再把此球放回袋中搅匀,由小亮从布袋中随机摸出一个小球,记下数字作为![]() 的值,请用树状图或表格列出
的值,请用树状图或表格列出![]() 、
、![]() 的所有可能的值,并求出直线
的所有可能的值,并求出直线![]() 不经过第四象限的概率.
不经过第四象限的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在正方形网格中以点A为圆心,AB为半径作圆A交网格于点C(如图(1)),过点C作圆的切线交网格于点D,以点A为圆心,AD为半径作圆交网格于点E(如图(2)).
问题:
(1)求∠ABC的度数;
(2)求证:△AEB≌△ADC;
(3)△AEB可以看作是由△ADC经过怎样的变换得到的?并判断△AED的形状(不用说明理由).
(4)如图(3),已知直线a,b,c,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形A′B′C′使三个顶点A′,B′,C′,分别在直线a,b,c上.要求写出简要的画图过程,不需要说明理由.


查看答案和解析>>
科目: 来源: 题型:
【题目】已知:射线![]() 交
交![]() 于点
于点![]() ,半径
,半径![]() ,
,![]() 是射线
是射线![]() 上的一个动点(不与
上的一个动点(不与![]() 、
、![]() 重合),直线
重合),直线![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 的切线交射线
的切线交射线![]() 于
于![]() .
.
![]() 图
图![]() 是点
是点![]() 在圆内移动时符合已知条件的图形,在点
在圆内移动时符合已知条件的图形,在点![]() 移动的过程中,请你通过观察、测量、比较,写出一条与
移动的过程中,请你通过观察、测量、比较,写出一条与![]() 的边、角或形状有关的规律,并说明理由;
的边、角或形状有关的规律,并说明理由;
![]() 请你在图
请你在图![]() 中画出点
中画出点![]() 在圆外移动时符合已知条件的图形,第
在圆外移动时符合已知条件的图形,第![]() 题中发现的规律是否仍然存在?说明理由.
题中发现的规律是否仍然存在?说明理由.
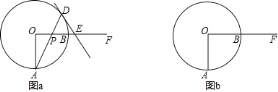
查看答案和解析>>
科目: 来源: 题型:
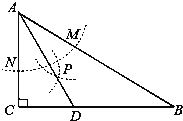
【题目】如图,△在ABC中,∠C=90°,∠B=30°,以A为圆心、任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,给出下列说法:①DM=DN;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3,其中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,给出下列说法:①DM=DN;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3,其中正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
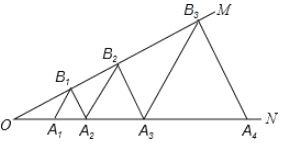
【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形.若OA1=1,则△A6B6A7的边长为( )
A.32B.24C.16D.8
查看答案和解析>>
科目: 来源: 题型:
【题目】某水果批发市场,草莓的批发价格是每箱![]() 元,苹果的批发价格是每箱
元,苹果的批发价格是每箱![]() 元.
元.
(1)若李心批发草莓,苹果共![]() 箱,刚好花费
箱,刚好花费![]() 元,则他购买草莓、苹果各多少箱.
元,则他购买草莓、苹果各多少箱.
(2)李心有甲,乙两个店铺,每个店铺在同一时间段内都能售出草莓,苹果两种水果合计![]() 箱,并且每售出一箱草莓和苹果,甲店铺获毛利润分别为
箱,并且每售出一箱草莓和苹果,甲店铺获毛利润分别为![]() 元和
元和![]() 元,乙店铺获毛利润分别为
元,乙店铺获毛利润分别为![]() 元和
元和![]() 元.现在,李心要将批发购进的
元.现在,李心要将批发购进的![]() 箱草莓,
箱草莓,![]() 箱苹果分配给每个店铺各
箱苹果分配给每个店铺各![]() 箱.设分配给甲店草莓
箱.设分配给甲店草莓![]() 箱.
箱.
①根据信息填表:
草莓数量(箱) | 苹果数量(箱) | 合计(箱) | |
甲店 |
|
| |
乙店 |
|
②设李心获取的总毛利润为![]() 元,
元,
(1)求![]() 与
与![]() 的函数关系式:
的函数关系式:
(2)若在保证乙店铺获得毛利润不少于![]() 元的前提下,应怎样分配水果,使总毛利润
元的前提下,应怎样分配水果,使总毛利润![]() 最大,最大的总毛利润是多少元.
最大,最大的总毛利润是多少元.
查看答案和解析>>
科目: 来源: 题型:
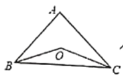
【题目】(1)如图所示,已知![]() 中,
中,![]() 的平分线相交于点
的平分线相交于点![]() ,试猜想
,试猜想![]() 与
与![]() 的关系,并证明.
的关系,并证明.
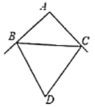
(2)如图所示,在![]() 中,
中,![]() 分别是
分别是![]() 的外角平分线,试猜想
的外角平分线,试猜想![]() 与
与![]() 的关系_____ (直接写结果不要证明)
的关系_____ (直接写结果不要证明)
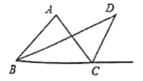
(3)如图所示,已知![]() 为
为![]() 的角平分线,
的角平分线,![]() 为
为![]() 外角
外角![]() 的平分线,且与
的平分线,且与![]() 交于点
交于点![]() ,试猜想
,试猜想![]() 与
与![]() 的关系_____ (直接写结果不要证明)
的关系_____ (直接写结果不要证明)
(1) (2)
(2)  (3)
(3) 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com