
科目: 来源: 题型:
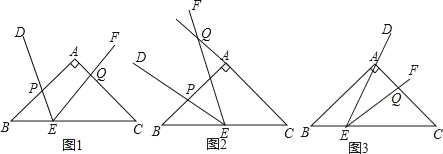
【题目】如图1,在等腰直角△ABC中,∠BAC=90°,AB=AC=2,点E是BC边上一点,∠DEF=45°且角的两边分别与边AB,射线CA交于点P,Q.
(1)如图2,若点E为BC中点,将∠DEF绕着点E逆时针旋转,DE与边AB交于点P,EF与CA的延长线交于点Q.设BP为x,CQ为y,试求y与x的函数关系式,并写出自变量x的取值范围;
(2)如图3,点E在边BC上沿B到C的方向运动(不与B,C重合),且DE始终经过点A,EF与边AC交于Q点.探究:在∠DEF运动过程中,△AEQ能否构成等腰三角形,若能,求出BE的长;若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,已知直线![]() 与直线
与直线![]() 相交于点
相交于点![]() 。
。
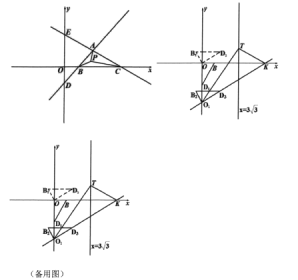
(1)求点![]() 的坐标;
的坐标;
(2)点![]() 是
是![]() 内部一点,连接
内部一点,连接![]() ,求
,求![]() 的最小值;
的最小值;
(3)将点![]() 向下平移一个单位得到点
向下平移一个单位得到点![]() ,连接
,连接![]() ,将
,将![]() 绕点
绕点![]() 旋转至
旋转至![]() 的位置,使
的位置,使![]() 轴,再将
轴,再将![]() 沿
沿![]() 轴上下平移得到
轴上下平移得到![]() ,在平移过程中,直线
,在平移过程中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,在直线
,在直线![]() 上任取一点
上任取一点![]() ,连接
,连接![]() ,
,![]() ,
,![]() 能否以
能否以![]() 为直线边构成等腰直角三角形?若能,请直接写出所有符合条件的
为直线边构成等腰直角三角形?若能,请直接写出所有符合条件的![]() 点的坐标,若不能,请说明理由。
点的坐标,若不能,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
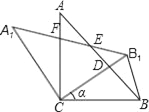
【题目】如图,△ABC中,∠ACB=90°,AC=BC=1,将△ABC绕点C逆时针旋转得到△A1B1C,旋转角为ɑ(0°<ɑ<90°),连接BB1.设CB1交AB于点D,A1B1分别交AB、AC于点E,F.
(1)求证:△BCD≌△A1CF;
(2)若旋转角ɑ为30°,
①请你判断△BB1D的形状;
②求CD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】开学初,为丰富教师们的业余生活,我校组织所有教师前往重庆大剧院观看演出。重庆大剧院的演出门票价格方案如下:1.票价根据座位区域不同定价不同,一区票价为120元/张,二区票价为100元/张;2.离退休教师各区均享受八折优惠。已知本次活动实到教师700人,若本次活动每人均购买二区票则需67200元。
(1)求参加本次活动的在职教师、离退休教师分别有多少人;
(2)为庆祝重阳节,重庆在大剧院调整了票价方案,将200张一区演出票票价每张降低了![]() 元,将全部二区演出票票价每张降低了
元,将全部二区演出票票价每张降低了![]() 元,离退休教师可在降价后仍享受八折优惠。若学校决定将200张一区演出票全部购入并优先发放给离退休教师和部分在职教师,其余教师均购买二区票,且校方希望总门票费用不超过66420元,求
元,离退休教师可在降价后仍享受八折优惠。若学校决定将200张一区演出票全部购入并优先发放给离退休教师和部分在职教师,其余教师均购买二区票,且校方希望总门票费用不超过66420元,求![]() 的最小值。
的最小值。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,直线
,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,
,![]() 的解析式为
的解析式为![]() ,
,![]() 的解析式为
的解析式为![]() 且
且![]() ,两直线的交点
,两直线的交点![]() 。
。

(1)求直线![]() 的解析式;
的解析式;
(2)求四边形![]() 的面积;
的面积;
(3)当![]() 时,直接写出
时,直接写出![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目: 来源: 题型:
【题目】在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是ycm2,设金色纸边的宽为xcm,要求纸边的宽度不得少于1cm,同时不得超过2cm.
(1)求出y关于x的函数解析式,并直接写出自变量的取值范围;
(2)此时金色纸边的宽应为多少cm时,这幅挂图的面积最大?求出最大面积的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】在建立平面直角坐标系的方格纸中,每个小方格都是边长为1的小正方形,△ABC的顶点均在格点上,点P的坐标为(﹣1,0),请按要求画图与作答.

(1)把△ABC绕点P旋转180°得△A′B′C′.
(2)把△ABC向右平移7个单位得△A″B″C″.
(3)△A′B′C′与△A″B″C″是否成中心对称,若是,找出对称中心P′,并写出其坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数y=x2+bx图象的对称轴为直线x=1,若关于x的一元二次方程x2+bx﹣t=0(t为实数)在﹣1≤x≤2的范围内有解,则t的取值范围是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com