
科目: 来源: 题型:
【题目】随着城际铁路的正式开通,从甲市经丙市到乙市的高铁里程比普快里程缩短了90km,运行时间减少了8h,已知甲市到乙市的普快列车里程为1220km.高铁平均时速是普快平均时速的2.5倍.
(1)求高铁列车的平均时速;
(2)某日王先生要从甲市去距离大约780km的丙市参加14:00召开的会议,如果他买到当日9:20从甲市到丙市的高铁票,而且从丙市火车站到会议地点最多需要1小时.试问在高铁列车准点到达的情况下,它能否在开会之前20分钟赶到会议地点?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,△ABC在正方形网格中,若点A的坐标为(0,3),按要求回答下列问题:
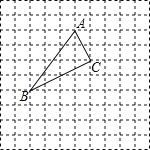
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点B和点C的坐标;
(3)作出△ABC关于x轴的对称图形△A′B′C′.(不用写作法)
(4)求△ABC的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】(2015镇江)
活动1:在一只不透明的口袋中装有标号为1,2,3的3个小球,这些球除标号外都相同,充分搅匀,甲、乙、丙三位同学丙→甲→乙的顺序依次从袋中各摸出一个球(不放回),摸到1号球胜出,计算甲胜出的概率.(注:丙→甲→乙表示丙第一个摸球,甲第二个摸球,乙最后一个摸球)
活动2:在一只不透明的口袋中装有标号为1,2,3,4的4个小球,这些球除标号外都相同,充分搅匀,请你对甲、乙、丙三名同学规定一个摸球顺序: → → ,他们按这个顺序从袋中各摸出一个球(不放回),摸到1号球胜出,则第一个摸球的同学胜出的概率等于 ,最后一个摸球的同学胜出的概率等于 .
猜想:在一只不透明的口袋中装有标号为1,2,3,…,n(n为正整数)的n个小球,这些球除标号外都相同,充分搅匀,甲、乙、丙三名同学从袋中各摸出一个球(不放回),摸到1号球胜出,猜想:这三名同学每人胜出的概率之间的大小关系.
你还能得到什么活动经验?(写出一个即可)
查看答案和解析>>
科目: 来源: 题型:
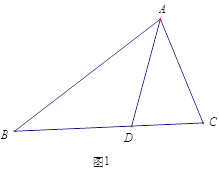
【题目】如图1,△ABC中,AD是∠BAC的角平分线,若AB=AC+CD.那么∠ACB 与∠ABC有怎样的数量关系? 小明通过观察分析,形成了如下解题思路:
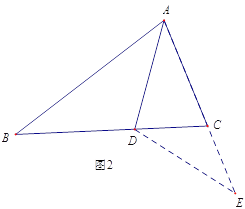
如图2,延长AC到E,使CE=CD,连接DE,由AB=AC+CD,可得AE=AB,又因为AD是∠BAC的平分线,可得△ABD≌△AED,进一步分析就可以得到∠ACB 与∠ABC的数量关系.
(1) 判定△ABD 与△AED 全等的依据是______________(SSS,SAS,ASA,AAS 从其中选择一个);
(2)∠ACB 与∠ABC的数量关系为:___________________
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN周长取最小值时,则∠MPN的度数为( )

A. 140° B. 100° C. 50° D. 40°
查看答案和解析>>
科目: 来源: 题型:
【题目】为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,东营市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)求该班的人数;
(2)请把折线统计图补充完整;
(3)求扇形统计图中,网络文明部分对应的圆心角的度数;
(4)小明和小丽参加了志愿服务活动,请用树状图或列表法求出他们参加同一服务活动的概率.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com