
科目: 来源: 题型:
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/公里计算,耗时费按y元/分钟计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与打车时间如表:
时间(分钟) | 里程数(公里) | 车费(元) | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
(1)求x,y的值;
(2)如果小华也用该打车方式,打车行驶了11公里,用了14分钟,那么小华的打车总费用为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC为4,面积为24,腰AC的垂直平分线EF分别交边AC,AB于点E,F,若D为BC边的中点,M为线段EF上一动点,则△CDM的周长的最小值为 ( )

A.8B.10C.12D.14
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点 A,B的坐标分别为(0,3),(1,0),△ABC是等腰直角三角形,∠ABC=90°.
(1)图1中,点C的坐标为 ;
(2)如图2,点D的坐标为(0,1),点E在射线CD上,过点B 作BF⊥BE交y轴于点F.
①当点E为线段CD的中点时,求点F的坐标;
②当点E在第二象限时,请直接写出F点纵坐标y的取值范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】电子跳蚤游戏盘是如图所示的△ABC,AB=AC=BC=5.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1= CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2= AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3= BP2;…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2016与点P2017之间的距离为_________.
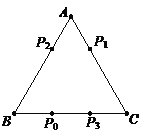
查看答案和解析>>
科目: 来源: 题型:
【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AF、BE是△ABC的中线,AF⊥BE于点P,像△ABC这样的三角形称为“中垂三角形”.设BC=a,AC=b,AB=c.
(特例探究)
(1)如图1,当tan∠PAB=1,c=2![]() 时,a= ,b= ;
时,a= ,b= ;
如图2,当∠PAB=30°,c=4时,a= ,b= ;
(归纳证明)
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
(拓展证明)
(3)如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=6![]() ,AB=6,求AF的长.
,AB=6,求AF的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].
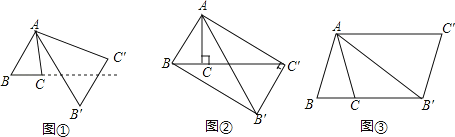
(1)如图①,对△ABC作变换[60°,![]() ]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线AB分别与两坐标轴交于点A(6,0),B(0,12),点C的坐标为(3,0)
(1)求直线AB的解析式;
(2)在线段AB上有一动点P.
①过点P分别作x,y轴的垂线,垂足分别为点E,F,若矩形OEPF的面积为16,求点P的坐标.
②连结CP,是否存在点P,使△ACP与△AOB相似?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点A坐标(0,6),AC⊥y轴,且AC=AO,点B,C横坐标相同,点D在AC上,tan∠AOD=![]() ,若反比例函数y=
,若反比例函数y=![]() (x>0)的图象经过点B、D.
(x>0)的图象经过点B、D.
(1)求:k及点B坐标;
(2)将△AOD沿着OD折叠,设顶点A的对称点A1的坐标是A1(m,n),求:代数式m+3n的值以及点A1的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料:数学课上,吴老师在求代数式x2﹣4x+5的最小值时,利用公式a2±2ab+b2=(a±b)2,对式子作如下变形:x2﹣4x+5=x2﹣4x+4+1=(x﹣2)2+1,
因为(x﹣2)2≥0,
所以(x﹣2)2+1≥1,
当x=2时,(x﹣2)2+1=1,
因此(x﹣2)2+1有最小值1,即x2﹣4x+5的最小值为1.
通过阅读,解下列问题:
(1)代数式x2+6x+12的最小值为 ;
(2)求代数式﹣x2+2x+9的最大或最小值;
(3)试比较代数式3x2﹣2x与2x2+3x﹣7的大小,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com