
科目: 来源: 题型:
【题目】学校对初2021级甲、乙两班各60名学生进行知识测试(满分60分),测试完成后分别抽取了12份成绩,整理分析过程如下,请补充完整.
(收集数据)
甲班12名学生测试成绩统计如下:
45,59,60,38,57,53,52,58,60,50,43,49
乙班12名学生测试成绩统计如下:
35,55,46,39,54,47,43,57,42,59,60,47
(整理数据)
按如下分数段整理,描述这两组样本数据
组别频数 |
|
|
|
|
|
甲 | 0 | 1 | 3 | 3 | 5 |
乙 | 2 | 2 | 3 | 1 | 4 |
(分析数据)
两组样本数据的平均数、众数、中位数、方差如下表所示:
班级 | 平均数 | 众数 | 中位数 |
甲 |
| 52.5 | |
乙 | 48.7 | 47 |
|
(1)![]() ,
,![]() ;
;
(2)若规定得分在40分及以上为合格,请估计乙班60名学生中知识测试合格的学生有多少人?
(3)你认为哪个班的学生知识测试的整体水平较好,请说明一条理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某超市销售一种饮料,平均每天可售出100箱,每箱利润120元.为了扩大销售,增加利润,超市准备适当降价.据测算,若每箱降价1元,每天可多售出2箱.
(1)如果要使每天销售饮料获利14000元,问每箱应降价多少元?
(2)每箱降价多少元超市每天获利最大?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读理解
材料一:已知在平面直角坐标系中有两点![]() ,
,![]() ,其两点间的距离公式为:
,其两点间的距离公式为:![]() ,当两点所在直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可化简为
,当两点所在直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可化简为![]() 或
或![]() ;
;
材料二:如图1,点![]() ,
,![]() 在直线
在直线![]() 的同侧,直线
的同侧,直线![]() 上找一点
上找一点![]() ,使得
,使得![]() 的值最小.解题思路:如图2,作点
的值最小.解题思路:如图2,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() 交直线
交直线![]() 于
于![]() ,则点
,则点![]() ,
,![]() 之间的距离即为
之间的距离即为![]() 的最小值.
的最小值.

请根据以上材料解决下列问题:
(1)已知点![]() 在平行于
在平行于![]() 轴的直线上,点
轴的直线上,点![]() 在第二象限的角平分线上,
在第二象限的角平分线上,![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)如图,在平面直角坐标系中,点![]() ,点
,点![]() ,请在直线
,请在直线![]() 上找一点
上找一点![]() ,使得
,使得![]() 最小,求出
最小,求出![]() 的最小值及此时点
的最小值及此时点![]() 的坐标.
的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,在边长为![]() 个单位长度的小正方形组成的方格中,点
个单位长度的小正方形组成的方格中,点![]() 都在格点上.
都在格点上.
(1)画出ΔABC绕着点B逆时针旋转90°得到的ΔA'B'C',并写出的A'的坐标__________
(2)在(1)的情况下,直接写出线段AA’的长度____________.
(3)在y轴上找一点P,使ΔPAB的周长最小,直接写出P的坐标_____________.

查看答案和解析>>
科目: 来源: 题型:
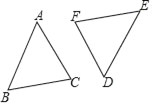
【题目】如图,△ABC和△DEF关于点O成中心对称.
(1)作出它们的对称中心O,并简要说明作法;
(2)若AB=6,AC=5,BC=4,求△DEF的周长;
(3)连接AF,CD,试判断四边形ACDF的形状,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
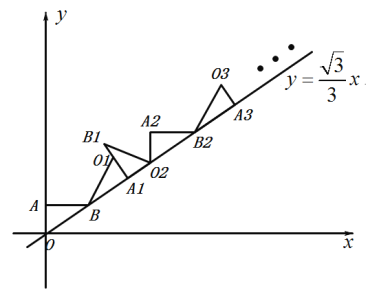
【题目】如图,在平面直角坐标系中,将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,使点
的位置,使点![]() 对应点
对应点![]() 落在直线
落在直线![]() 上,再将
上,再将![]() 绕点
绕点![]() 旋转到
旋转到![]() 的位置,使点
的位置,使点![]() 的对应点
的对应点![]() 落在直线
落在直线![]() 上,依次进行下去…,若点
上,依次进行下去…,若点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的横坐标为___________.
的横坐标为___________.
查看答案和解析>>
科目: 来源: 题型:
【题目】(多选)在同一条道路上,甲车从![]() 地到
地到![]() 地,乙车从
地,乙车从![]() 地到
地到![]() 地,两车同时出发,乙车先到达目的地,图中的折线段表示甲,乙两车之间的距离
地,两车同时出发,乙车先到达目的地,图中的折线段表示甲,乙两车之间的距离![]() (千米)与行驶时间
(千米)与行驶时间![]() (小时)的函数关系,下列说法正确的是( )
(小时)的函数关系,下列说法正确的是( )

A.甲乙两车出发2小时后相遇
B.甲车速度是40千米/小时
C.相遇时乙车距离![]() 地100千米
地100千米
D.乙车到![]() 地比甲车到
地比甲车到![]() 地早
地早![]() 小时
小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com