
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的反称点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=2r,则称P′为点P关于⊙C的反称点,如图为点P及其关于⊙C的反称点P′的示意图.
特别地,当点P′与圆心C重合时,规定CP′=0.
(1)当⊙O的半径为1时.
①分别判断点M(2,1),N(![]() ,0),T(1,
,0),T(1, ![]() )关于⊙O的反称点是否存在?若存在,求其坐标;
)关于⊙O的反称点是否存在?若存在,求其坐标;
②点P在直线y=﹣x+2上,若点P关于⊙O的反称点P′存在,且点P′不在x轴上,求点P的横坐标的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线y=﹣![]() x+2
x+2![]() 与x轴、y轴分别交于点A,B,若线段AB上存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
与x轴、y轴分别交于点A,B,若线段AB上存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】某大型水果超市销售无锡水蜜桃,根据前段时间的销售经验,每天的售价x(元/箱)与销售量y(箱)有如表关系:
每箱售价x(元) | 68 | 67 | 66 | 65 | … | 40 |
每天销量y(箱) | 40 | 45 | 50 | 55 | … | 180 |
已知y与x之间的函数关系是一次函数.
(1)求y与x的函数解析式;
(2)水蜜桃的进价是40元/箱,若该超市每天销售水蜜桃盈利1600元,要使顾客获得实惠,每箱售价是多少元?
(3)七月份连续阴雨,销售量减少,超市决定采取降价销售,所以从7月17号开始水蜜桃销售价格在(2)的条件下,下降了m%,同时水蜜桃的进货成本下降了10%,销售量也因此比原来每天获得1600元盈利时上涨了2m%(m<100),7月份(按31天计算)降价销售后的水蜜桃销售总盈利比7月份降价销售前的销售总盈利少7120元,求m的值.
查看答案和解析>>
科目: 来源: 题型:
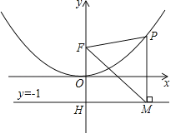
【题目】二次函数图象的顶点在原点O,且经过点A(1,![]() );点F(0,1)在y轴上.直线y=-1与y轴交于点H.
);点F(0,1)在y轴上.直线y=-1与y轴交于点H.
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=-1交于点M,求证:点M到∠OFP两边距离相等.
查看答案和解析>>
科目: 来源: 题型:
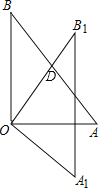
【题目】已知:如图,在△AOB中,∠AOB=90°,AO=3cm,BO=4cm,将△AOB绕顶点O,按顺时针方向旋转到△A1OB1处,此时线段OB1与AB的交点D恰好为AB的中点,则线段B1D的长度为( )
A.![]() cmB.1cmC.2cmD.
cmB.1cmC.2cmD.![]() cm
cm
查看答案和解析>>
科目: 来源: 题型:
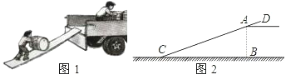
【题目】如图1是工人将货物搬运上货车常用的方法,把一块木板斜靠在货车车厢的尾部,形成一个斜坡,货物通过斜坡进行搬运.根据经验,木板与地面的夹角为20°(即图2中∠ACB=20°)时最为合适,已知货车车厢底部到地面的距离AB=1.5m,木板超出车厢部分AD=0.5m,请求出木板CD的长度?
(参考数据:sin20°≈0.3420,cos20°≈0.9397,精确到0.1m)
查看答案和解析>>
科目: 来源: 题型:
【题目】商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到奶汁的概率是 ;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶汁的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门统计绘制出2017年“五一”长假期间旅游情况统计图,根据以下信息解答下列问题:
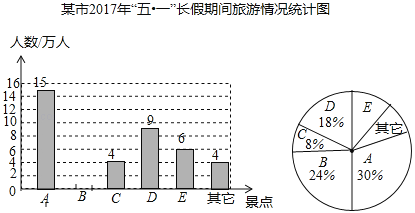
(1)2017年“五一”期间,该市周边景点共接待游客 万人,扇形统计图中A景点所对应的圆心角的度数是 ,并补全条形统计图.
(2)根据近几年到该市旅游人数增长趋势,预计2018年“五一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?
查看答案和解析>>
科目: 来源: 题型:
【题目】在正方形方格纸中,我们把顶点都在“格点”上的三角形称为“格点三角形“,如图,△ABC是一个格点三角形,点A的坐标为(﹣1,2).
(1)点B的坐标为 ,△ABC的面积为 ;
(2)在所给的方格纸中,请你以原点O为位似中心,将△ABC放大为原来的2倍,放大后点A、B的对应点分别为A1、B1,点B1在第一象限;
(3)在(2)中,若P(a,b)为线段AC上的任一点,则放大后点P的对应点P1的坐标为 .

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC和△DCB中,AC与BD相交于点O,下列四组条件中,不能证明△ABC≌△DCB的是( )

A.AB=DC,AC=DBB.AB=DC,∠ABC=∠DCB
C.BO=CO,∠A=∠DD.∠ABD=∠DCA,∠A=∠D
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com