
科目: 来源: 题型:
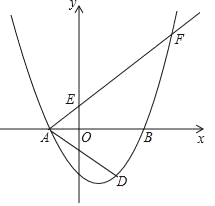
【题目】如图,在平面直角坐标系xOy中,已知抛物线y= ![]() 与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,﹣3),经过点A的射线AM与y轴相交于点E,与抛物线的另一个交点为F,且
与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,﹣3),经过点A的射线AM与y轴相交于点E,与抛物线的另一个交点为F,且![]() .
.
(1)求这条抛物线的表达式,并写出它的对称轴;
(2)求∠FAB的余切值;
(3)点D是点C关于抛物线对称轴的对称点,点P是y轴上一点,且∠AFP=∠DAB,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】为推进节能减排,发展低碳经济,某市“用电大户”用480万元购得“变频调速技术”后,进一步投入资金1520万元购买配套设备,以提高用电效率达到节约用电的目的.已知该“用电大户”生产的产品“草甘磷”每件成本费为40元.经过市场调研发现:该产品的销售单价,需定在100元到300元之间较为合理.当销售单价定为100元时,年销售量为20万件;当销售单价超过100元,但不超过200元时,每件新产品的销售价格每增加10元,年销售量将减少0.8万件;当销售单价超过200元,但不超过300元时,每件产品的销售价格在200元的基础上每增加10元,年销售量将减少1万件.设销售单价为x(元),年销售量为y(万件),年获利为w(万元).(年获利=年销售额-生产成本-节电投资)
(1)直接写出y与x之间的函数关系式;
(2)求第一年的年获利w与x间的函数关系式,并说明投资的第一年,该“用电大户”是盈利还是亏损?若盈利,最大利润是多少?若亏损,最少亏损是多少?
(3)若该“用电大户”把“草甘磷”的销售单价定在超过100元,但不超过200元的范围内,并希望到第二年底,除去第一年的最大盈利(或最小亏损)后,两年的总盈利为1842万元,请你确定此时销售单价.在此情况下,要使产品销售量最大,销售单价应定为多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知四边形ABCD是正方形,点B,C分别在直线![]() 和
和![]() 上,点A,D是x轴上两点.
上,点A,D是x轴上两点.

(1)若此正方形边长为2,k=_______.
(2)若此正方形边长为a,k的值是否会发生变化?若不会发生变化,请说明理由;若会发生变化,求出a的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知正比例函数图象上一个点A到x轴的距离为4,点A的横坐标为-2,请回答下列问题:
(1)求这个正比例函数;
(2)这个正比例函数图象经过哪几个象限?
(3)这个正比例函数的函数值y是随着x的增大而增大?还是随着x的增大而减小?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于点C.抛物线
与x轴交于点A,与y轴交于点C.抛物线![]() 经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
经过A,C两点,且与x轴交于另一点B(点B在点A右侧).

(1)求抛物线的解析式及点B坐标;
(2)若点M是线段BC上的一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;
(3)试探究当ME取最大值时,在抛物线上、x轴下方是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图1,四边形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边的中点,连接
边的中点,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证:![]() .(
.(![]() 表示面积)
表示面积)
(2)如图2,在![]() 中,过
中,过![]() 边的中点
边的中点![]() 任意作直线
任意作直线![]() ,交
,交![]() 边于点
边于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,试比较
,试比较![]() 与
与![]() 的面积,并说明理由.
的面积,并说明理由.
(3)如图3,在平面直角坐标系中,已知一次函数![]() 的图像过点
的图像过点![]() 且分别于
且分别于![]() 轴正半轴,
轴正半轴,![]() 轴正半轴交于点
轴正半轴交于点![]() 、
、![]() ,请问
,请问![]() 的面积是否存在最小值?若存在,求出此时一次函数关系式;若不存在,请说明理由.
的面积是否存在最小值?若存在,求出此时一次函数关系式;若不存在,请说明理由.
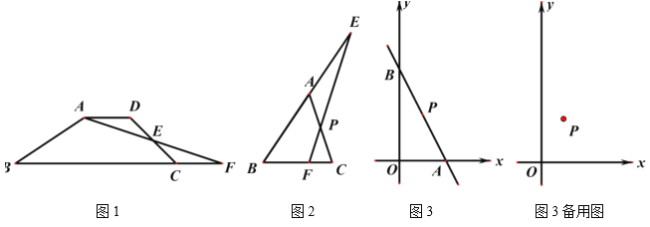
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在一块三角形区域ABC中,∠C=90°,边AC=8m,BC=6m,现要在△ABC内建造一个矩形水池DEFG,如图的设计方案是使DE在AB上.
(1)求△ABC中AB边上的高h;
(2)设DG=x,当x取何值时,水池DEFG的面积(S)最大?
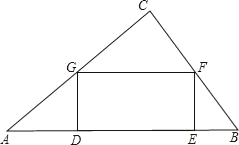
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C,已知点A(﹣1,0),点C(0,2)
x2+bx+c与x轴交于A、B两点,与y轴交于点C,已知点A(﹣1,0),点C(0,2)
(1)求抛物线的函数解析式;
(2)若D是抛物线位于第一象限上的动点,求△BCD面积的最大值及此时点D的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)判断△BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com