
科目: 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的性质.
的性质.
(1)先从简单情况开始探究:
① 当函数为![]() 时,
时, ![]() 随
随![]() 增大而 (填“增大”或“减小”);
增大而 (填“增大”或“减小”);
② 当函数为![]() 时,它的图象与直线
时,它的图象与直线![]() 的交点坐标为 ;
的交点坐标为 ;
(2)当函数为![]() 时,
时,
下表为其y与x的几组对应值.
x | … |
| 0 | 1 |
| 2 |
| 3 | 4 |
| … |
y | … |
|
| 1 |
| 2 |
| 3 | 7 |
| … |

①如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象;
②根据画出的函数图象,写出该函数的一条性质: .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,隧道的截面由抛物线ADC和矩形AOBC构成,矩形的长OB是12m,宽OA是4m.拱顶D到地面OB的距离是10m.若以O原点,OB所在的直线为x轴,OA所在的直线为y轴,建立直角坐标系.
(1)画出直角坐标系xOy,并求出抛物线ADC的函数表达式;
(2)在抛物线型拱壁E、F处安装两盏灯,它们离地面OB的高度都是8m,则这两盏灯的水平距离EF是多少米?

查看答案和解析>>
科目: 来源: 题型:
【题目】“军运会”期间,某纪念品店老板用5000元购进一批纪念品,由于深受顾客喜爱,很快售完,老板又用6000元购进同样数目的这种纪念品,但第二次每个进价比第一次每个进价多了2元.
(1)求该纪念品第一次每个进价是多少元?
(2)老板以每个15元的价格销售该纪念品,当第二次纪念品售出![]() 时,出现了滞销,于是决定降价促销,若要使第二次的销售利润不低于900元,剩余的纪念品每个售价至少要多少元?
时,出现了滞销,于是决定降价促销,若要使第二次的销售利润不低于900元,剩余的纪念品每个售价至少要多少元?
查看答案和解析>>
科目: 来源: 题型:
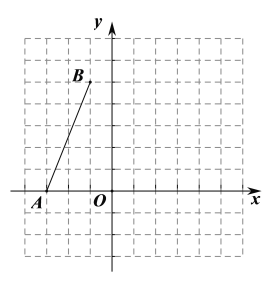
【题目】如图,在平面直角坐标系中,点![]() ,点
,点![]() .
.
(1)①画出线段![]() 关于
关于![]() 轴对称的线段
轴对称的线段![]() ;
;
②在![]() 轴上找一点
轴上找一点![]() 使
使![]() 的值最小(保留作图痕迹);
的值最小(保留作图痕迹);
(2)按下列步骤,用不带刻度的直尺在线段![]() 找一点
找一点![]() 使
使![]() .
.
①在图中取点![]() ,使得
,使得![]() ,且
,且![]() ,则点
,则点![]() 的坐标为___________;
的坐标为___________;
②连接![]() 交
交![]() 于点
于点![]() ,则点
,则点![]() 即为所求.
即为所求.
查看答案和解析>>
科目: 来源: 题型:
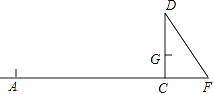
【题目】已知:CD为一幢3米高的温室,其南面窗户的底框G距地面1米,CD在地面上留下的最大影长CF为2米,现欲在距C点7米的正南方A点处建一幢12米高的楼房AB(设A,C,F在同一水平线上).
(1)按比例较精确地作出高楼AB及它的最大影长AE;
(2)问若大楼AB建成后是否影响温室CD的采光,试说明理由.
查看答案和解析>>
科目: 来源: 题型:
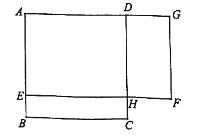
【题目】如图, ![]() 是一块边长为4米的正方形苗圃,园林部门将其改造为矩形
是一块边长为4米的正方形苗圃,园林部门将其改造为矩形![]() 的形状,其中点
的形状,其中点![]() 在
在![]() 边上,点
边上,点![]() 在
在![]() 的延长线上,
的延长线上, ![]() 设
设![]() 的长为
的长为![]() 米,改造后苗圃
米,改造后苗圃![]() 的面积为
的面积为![]() 平方米.
平方米.
(1) ![]() 与
与![]() 之间的函数关系式为 (不需写自变量的取值范围);
之间的函数关系式为 (不需写自变量的取值范围);
(2)根据改造方案,改造后的矩形苗圃![]() 的面积与原正方形苗圃
的面积与原正方形苗圃![]() 的面积相等,请问此时
的面积相等,请问此时![]() 的长为多少米?
的长为多少米?
查看答案和解析>>
科目: 来源: 题型:
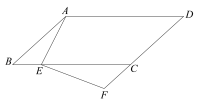
【题目】如图,在□ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.
(1)求证:△ABE∽△ECF;
(2)若AB=5,AD=8,BE=2,求FC的长。
查看答案和解析>>
科目: 来源: 题型:
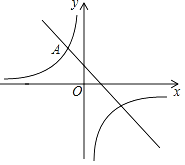
【题目】如图,在平面直角坐标系xOy中,反比例函数y=![]() 的图象与一次函数y=﹣x+1的图象的一个交点为A(﹣1,m).
的图象与一次函数y=﹣x+1的图象的一个交点为A(﹣1,m).
(1)求这个反比例函数的表达式;
(2)如果一次函数y=﹣x+1的图象与x轴交于点B(n,0),请确定当x<n时,对应的反比例函数y=![]() 的值的范围.
的值的范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数![]() .
.
(![]() )将
)将![]() 化成
化成![]() 的形式.
的形式.
(![]() )与
)与![]() 轴的交点坐标是__________,与
轴的交点坐标是__________,与![]() 轴的交点坐标是__________.
轴的交点坐标是__________.
(![]() )在坐标系中利用描点法画出此抛物线.
)在坐标系中利用描点法画出此抛物线.
|
|
| |||||
|
|
|
(![]() )不等式
)不等式![]() 的解集是__________.
的解集是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com