
科目: 来源: 题型:
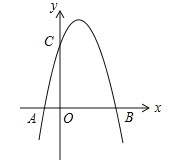
【题目】如图,二次函数![]() 的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点.
的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点.
(1)求m的值及C点坐标;
(2)在直线BC上方的抛物线上是否存在一点M,使得它与B,C两点构成的三角形面积最大,若存在,求出此时M点坐标;若不存在,请简要说明理由;
(3)P为抛物线上一点,它关于直线BC的对称点为Q.
①当四边形PBQC为菱形时,求点P的坐标;
②点P的横坐标为t(0<t<4),当t为何值时,四边形PBQC的面积最大,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
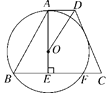
【题目】如图,梯形ABCD中,AD∥BC,AE⊥BC于点E,∠ADC的平分线交AE于点O,以点O为圆心,OA为半径的圆经过点B,交BC于另一点F.
(1)求证:CD与⊙O相切;
(2)若BF=24,OE=5,求tan∠ABC的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标![]() 中,正比例函数
中,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象经过点
的图象经过点![]() .
.
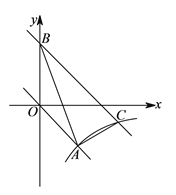
(![]() )分别求这两个函数的表达式.
)分别求这两个函数的表达式.
(![]() )将直线
)将直线![]() 向上平移
向上平移![]() 个单位长度后与
个单位长度后与![]() 轴交于点
轴交于点![]() ,与反比例函数图象在第四象限内的交点为
,与反比例函数图象在第四象限内的交点为![]() ,连接
,连接![]() 、
、![]() ,求点
,求点![]() 的坐标及
的坐标及![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
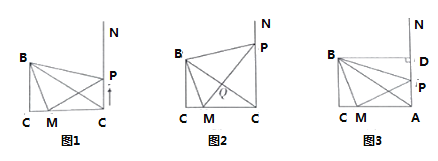
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 在
在![]() 上,且
上,且![]() ,过点
,过点![]() 作射线
作射线![]() (AN与BC在AC同侧),若动点
(AN与BC在AC同侧),若动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 匀速运动,运动速度为
匀速运动,运动速度为![]() /
/![]() ,设点
,设点![]() 运动时间为
运动时间为![]() 秒.
秒.
(1)经过_______秒时,![]() 是等腰直角三角形?
是等腰直角三角形?
(2)当![]() 于点
于点![]() 时,求此时
时,求此时![]() 的值;
的值;
(3)过点![]() 作
作![]() 于点
于点![]() ,已知
,已知![]() ,请问是否存在点
,请问是否存在点![]() ,使
,使![]() 是以
是以![]() 为腰的等腰三角形?对存在的情况,请求出t的值,对不存在的情况,请说明理由.
为腰的等腰三角形?对存在的情况,请求出t的值,对不存在的情况,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
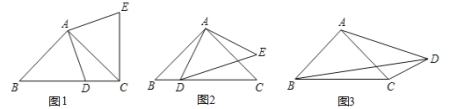
【题目】(1)问题:如图![]() 在
在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边上一点(不与点
边上一点(不与点![]() ,
,![]() 重合),连接
重合),连接![]() ,过点
,过点![]() 作
作![]() ,并满足
,并满足![]() ,连接
,连接![]() .则线段
.则线段![]() 和线段
和线段![]() 的数量关系是_______,位置关系是_______.
的数量关系是_______,位置关系是_______.
(2)探索:如图![]() ,当
,当![]() 点为
点为![]() 边上一点(不与点
边上一点(不与点![]() ,
,![]() 重合),
重合),![]() 与
与![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,
,![]() ,
,![]() .试探索线段
.试探索线段![]() ,
,![]() ,
,![]() 之间满足的等量关系,并证明你的结论;
之间满足的等量关系,并证明你的结论;
(3)拓展:如图![]() ,在四边形
,在四边形![]() 中,
中,![]() ,若
,若![]() ,
,![]() ,请直接写出线段
,请直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】为厉行节能减排,倡导绿色出行,今年3月以来.“共享单车”(俗称“小黄车”)公益活动登陆我市中心城区,某公司拟在甲、乙两个街道社区投放一批“小黄车”,这批自行车包括A、B两种不同款型,请回答下列问题:
问题1:单价
该公司早期在甲街区进行了试点投放,共投放A、B两型自行车各50辆,投放成本共计7500元,其中B型车的成本单价比A型车高10元,A、B两型自行车的单价各是多少?
问题2:投放方式
该公司决定采取如下投放方式:甲街区每1000人投放a辆“小黄车”,乙街区每1000人投放![]() 辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
查看答案和解析>>
科目: 来源: 题型:
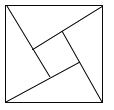
【题目】如图的图形取材于我国古代数学家赵爽的《勾股圆方图》也称(《赵爽弦图》),它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是![]() ,小正方形的面积是
,小正方形的面积是![]() ,直角三角形较短的直角边为
,直角三角形较短的直角边为![]() ,较长的直角边为
,较长的直角边为![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】风电已成为我国继煤电、水电之后的第三大电源,风电机组主要由塔杆和叶片组成(如图1),图2是从图1引出的平面图.假设你站在A处测得塔杆顶端C的仰角是55°,沿HA方向水平前进43米到达山底G处,在山顶B处发现正好一叶片到达最高位置,此时测得叶片的顶端D(D、C、H在同一直线上)的仰角是45°.已知叶片的长度为35米(塔杆与叶片连接处的长度忽略不计),山高BG为10米,BG⊥HG,CH⊥AH,求塔杆CH的高.(参考数据:tan55°≈1.4,tan35°≈0.7,sin55°≈0.8,sin35°≈0.6)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com