
科目: 来源: 题型:
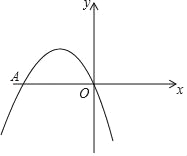
【题目】如图,二次函数y=ax2﹣4x+c的图象经过坐标原点,与x轴交于点A(﹣4,0).
(1)该二次函数的关系式是 ,顶点坐标 .
(2)根据图象回答:当x满足 时,y>0;
(3)在抛物线上存在点P,满足S△AOP=8,请直接写出点P的坐标 .
查看答案和解析>>
科目: 来源: 题型:
【题目】商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到奶汁的概率是 ;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶汁的概率.
查看答案和解析>>
科目: 来源: 题型:
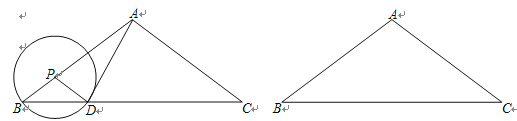
【题目】如图,已知在△ABC中,AB=AC=5,cosB=![]() ,P是边AB上一点,以P为圆心,PB为半径的⊙P与边BC的另一个交点为D,联结PD、AD.
,P是边AB上一点,以P为圆心,PB为半径的⊙P与边BC的另一个交点为D,联结PD、AD.
(1)求△ABC的面积;
(2)设PB=x,△APD的面积为y,求y关于x的函数关系式,并写出定义域;
(3)如果△APD是直角三角形,求PB的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】平面直角坐标系xOy中(如图),已知抛物线y=ax2+bx+3与y轴相交于点C,与x轴正半轴相交于点A,OA=OC,与x轴的另一个交点为B,对称轴是直线x=1,顶点为P.
(1)求这条抛物线的表达式和顶点P的坐标;
(2)抛物线的对称轴与x轴相交于点M,求∠PMC的正切值;
(3)点Q在y轴上,且△BCQ与△CMP相似,求点Q的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )

A. 15 B. 18 C. 21 D. 24
查看答案和解析>>
科目: 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ACB=90°,AC > BC,CD是Rt△ABC的高,E是AC的中点,ED的延长线与CB的延长线相交于点F.
(1)求证:DF是BF和CF的比例中项;
(2)在AB上取一点G,如果AE·AC=AG·AD,求证:EG·CF=ED·DF.

查看答案和解析>>
科目: 来源: 题型:
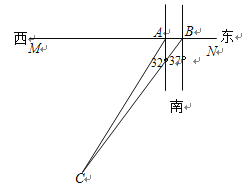
【题目】如图,MN是一条东西方向的海岸线,在海岸线上的A处测得一海岛在南偏西32°的方向上,向东走过780米后到达B处,测得海岛在南偏西37°的方向,求小岛到海岸线的距离.
(参考数据:tan37°= cot53°≈0.755,cot37°= tan53°≈1.327,tan32°= cot58°≈0.625,cot32°= tan58°≈1.600.)
查看答案和解析>>
科目: 来源: 题型:
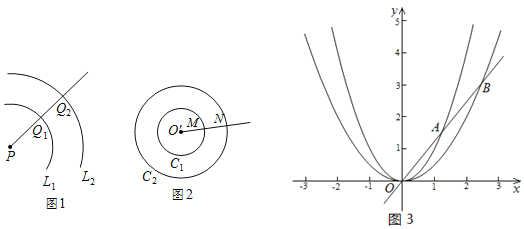
【题目】如图1,对于平面内的点P和两条曲线![]() 、
、![]() 给出如下定义:若从点P任意引出一条射线分别与
给出如下定义:若从点P任意引出一条射线分别与![]() 、
、![]() 交于
交于![]() 、
、![]() ,总有
,总有![]() 是定值,我们称曲线
是定值,我们称曲线![]() 与
与![]() “曲似”,定值
“曲似”,定值![]() 为“曲似比”,点P为“曲心”.
为“曲似比”,点P为“曲心”.
例如:如图2,以点![]() 为圆心,半径分别为
为圆心,半径分别为![]() 、
、![]() 都是常数
都是常数![]() 的两个同心圆
的两个同心圆![]() 、
、![]() ,从点
,从点![]() 任意引出一条射线分别与两圆交于点M、N,因为总有
任意引出一条射线分别与两圆交于点M、N,因为总有![]() 是定值,所以同心圆
是定值,所以同心圆![]() 与
与![]() 曲似,曲似比为
曲似,曲似比为![]() ,“曲心”为
,“曲心”为![]() .
.
![]() 在平面直角坐标系xOy中,直线
在平面直角坐标系xOy中,直线![]() 与抛物线
与抛物线![]() 、
、![]() 分别交于点A、B,如图3所示,试判断两抛物线是否曲似,并说明理由;
分别交于点A、B,如图3所示,试判断两抛物线是否曲似,并说明理由;
![]() 在
在![]() 的条件下,以O为圆心,OA为半径作圆,过点B作x轴的垂线,垂足为C,是否存在k值,使
的条件下,以O为圆心,OA为半径作圆,过点B作x轴的垂线,垂足为C,是否存在k值,使![]() 与直线BC相切?若存在,求出k的值;若不存在,说明理由;
与直线BC相切?若存在,求出k的值;若不存在,说明理由;
![]() 在
在![]() 、
、![]() 的条件下,若将“
的条件下,若将“![]() ”改为“
”改为“![]() ”,其他条件不变,当存在
”,其他条件不变,当存在![]() 与直线BC相切时,直接写出m的取值范围及k与m之间的关系式.
与直线BC相切时,直接写出m的取值范围及k与m之间的关系式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形ABCD中,E是BC边上一点,连接AE,延长CB至点F,使![]() ,过点F作
,过点F作![]() 于点H,射线FH分别交AB、CD于点M、N,交对角线AC于点P,连接AF.
于点H,射线FH分别交AB、CD于点M、N,交对角线AC于点P,连接AF.
![]() 依题意补全图形;
依题意补全图形;
![]() 求证:
求证:![]() ;
;
![]() 判断线段FM与PN的数量关系,并加以证明.
判断线段FM与PN的数量关系,并加以证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com