
科目: 来源: 题型:
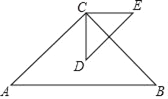
【题目】已知:如图,点D是等腰直角△ABC的重心,其中∠ACB=90°,将线段CD绕点C逆时针旋转90°得到线段CE,连结DE,若△ABC的周长为6,则△DCE的周长为( )
A. 2![]() B. 2
B. 2![]() C. 4 D. 3
C. 4 D. 3![]()
查看答案和解析>>
科目: 来源: 题型:
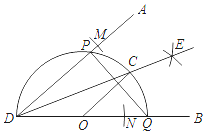
【题目】已知∠ADB,作图.
步骤1:以点D为圆心,适当长为半径画弧,分别交DA、DB于点M、N;再分别以点M、N为圆心,大于![]() MN长为半径画弧交于点E,画射线DE.
MN长为半径画弧交于点E,画射线DE.
步骤2:在DB上任取一点O,以点O为圆心,OD长为半径画半圆,分别交DA、DB、DE于点P、Q、C;
步骤3:连结PQ、OC.
则下列判断:①![]() ;②OC∥DA;③DP=PQ;④OC垂直平分PQ,其中正确的结论有( )
;②OC∥DA;③DP=PQ;④OC垂直平分PQ,其中正确的结论有( )
A. ①③④ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目: 来源: 题型:
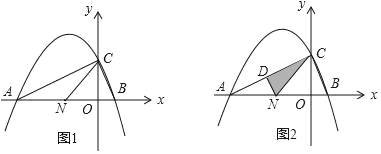
【题目】如图1,抛物线y=﹣![]() x2+bx+c(a≠0)与x轴交于A(﹣4,0)、B(1,0)两点,与y轴交于C点,对称轴x=﹣
x2+bx+c(a≠0)与x轴交于A(﹣4,0)、B(1,0)两点,与y轴交于C点,对称轴x=﹣![]() ,点N(n,0)是线段AB上的一个动点(N与A、B两点不重合),请回答下列问题:
,点N(n,0)是线段AB上的一个动点(N与A、B两点不重合),请回答下列问题:
(1)求出抛物线的解析式,并写出C点的坐标;
(2)试求出当n为何值时,△ANC恰能构成是等腰三角形.
(3)如图2,过N作NF∥BC,与AC相交于D点,连结CN,请问在N点的运动过程中,△CDN的面积是否存在最大值;若存在,试求出该最大面积,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
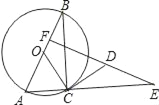
【题目】如图,⊙O是Rt△ABC的外接圆,AB为直径,∠ABC=30°,CD是⊙O的切线,E为AC延长线上一点,ED⊥AB于F.
(1)判断△DCE的形状;
(2)设⊙O的半径为1,且OF=![]() ,求证:△DCE≌△OCB.
,求证:△DCE≌△OCB.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了编撰祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“山重水复疑无路”.
(1)小明回答该问题时,对第二个字是选“重”还是选“穷”难以抉择,若随机选择其中一个,则小明回答正确的概率是 ;
(2)小丽回答该问题时,对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.

查看答案和解析>>
科目: 来源: 题型:
【题目】(6分)如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC.
(1)作出△ABC以O为旋转中心,顺时针旋转90°的△A1B1C1,(只画出图形).
(2)作出△ABC关于原点O成中心对称的△A2B2C2,(只画出图形),写出B2和C2的坐标.

查看答案和解析>>
科目: 来源: 题型:
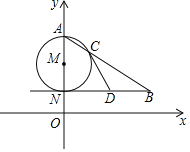
【题目】如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.
查看答案和解析>>
科目: 来源: 题型:
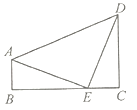
【题目】1876年,美国总统Garfield用如图所示的两个全等的直角三角形证明了勾股定理,若图中![]() ,
,![]() ,
,![]() ,则下面结论错误的是( )
,则下面结论错误的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() 是等腰直角三角形
是等腰直角三角形
查看答案和解析>>
科目: 来源: 题型:
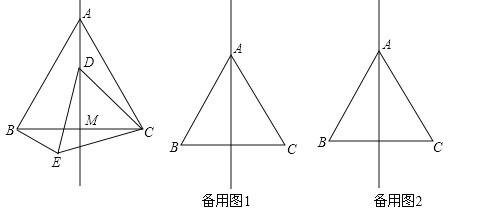
【题目】如图,在等边△ABC中,线段AM为BC边上的中线.动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.
(1)求∠CAM的度数;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
(3)当动D在直线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com