
科目: 来源: 题型:
【题目】小明同学要测量学校的国旗杆BD的高度.如图,学校的国旗杆与教学楼之间的距AB=20m.小明在教学楼三层的窗口C测得国旗杆顶点D的仰角为14°,旗杆底部B的俯角为22°.
(1)求∠BCD的大小.
(2)求国旗杆BD的高度(结果精确到1m.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin14°≈0.24,cos14°≈0.97,tan14°≈0.25)

查看答案和解析>>
科目: 来源: 题型:
【题目】一天早上小华步行上学,他离开家后不远便发现数学书忘在了家里,于是以相同的速度回家去拿,到家后发现弟弟把牛奶洒在了地上,就放下手中的东西,收拾好后才离开.为了不迟到,小华跑步到了学校,则小华离学校的距离y与时间t之间的函数关系的大致图象是( )
A.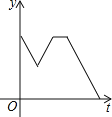 B.
B.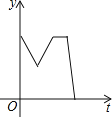 C.
C.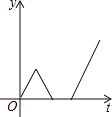 D.
D.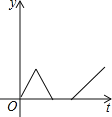
查看答案和解析>>
科目: 来源: 题型:
【题目】新华中学暑假要进行全面维修,有甲、乙两个工程队共同完成,甲队单独完成这项工程所需天数是乙队单独完成所需天数的![]() ,若由甲队先做10天,剩下的工程再由甲、乙两队合作,再做30天可以完成.
,若由甲队先做10天,剩下的工程再由甲、乙两队合作,再做30天可以完成.
(1)求甲、乙两队单独完成这项工程各需多少秀?
(2)已知甲队每天的施工费用为0.84万元,乙队每天的施工费用为0.56万元,若由甲、乙两队合作,则工程预算的施工费用50万元是否够用?若不够用,需追加多少万元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠BAC的度数为( )

A. 40° B. 45° C. 60° D. 70°
查看答案和解析>>
科目: 来源: 题型:
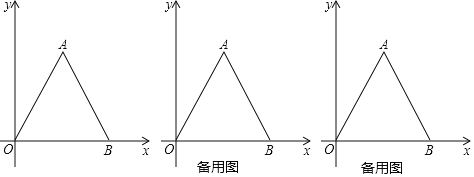
【题目】如图,在平面直角坐标系中,等边三角形△ABO的边长为4.
(1)求点A的坐标.
(2)若点P从点O出发以每秒1个单位的速度沿x轴正方向运动,运动时间为t秒,△PAB的面积为S,求S与t的关系式,并直接写出t的范围.
(3)在(2)的条件下,当点P在点B的右侧时,若S=![]() ,在平面内是否存在点Q,使点P、Q、A、B围成的四边形是平行四边形?若存在,求出点Q坐标;若不存在,请说明理由.
,在平面内是否存在点Q,使点P、Q、A、B围成的四边形是平行四边形?若存在,求出点Q坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
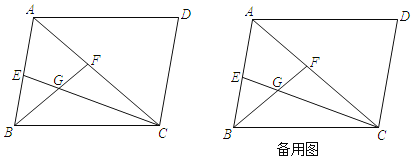
【题目】四边形ABCD为平行四边形,AC为对角线,∠BAC=60°,CE、BF分别∠ACB、∠ABC的角平分线,CE、BF相交于G;
(1)求∠CGF的度数;
(2)求证:BE+CF=BC;
(3)若BE:CF=1:2,EG=2![]() ,求平行四边形ABCD的面积.
,求平行四边形ABCD的面积.
查看答案和解析>>
科目: 来源: 题型:
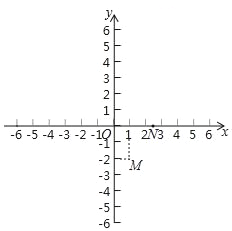
【题目】已知抛物线y=ax2+bx+c(x为任意实数)经过下图中两点M(1,﹣2)、N(m,0),其中M为抛物线的顶点,N为定点.下列结论:
①若方程ax2+bx+c=0的两根为x1,x2(x1<x2),则﹣1<x1<0,2<x2<3;
②当x<m时,函数值y随自变量x的减小而减小.
③a>0,b<0,c>0.
④垂直于y轴的直线与抛物线交于C、D两点,其C、D两点的横坐标分别为s、,则s+t=2.
其中正确的是( )
A. ①② B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学为了创建书香校园,去年购买了一批图书,其中科普书的单价比文学书的单价多4元,用1200元购买的科普书与用800元购买的文学书数量相等.
(1)求去年购买的文学书和科普书的单价各是多少元?
(2)若今年文学书的单价比去年提高了25%,科普书的单价与去年相同,这所中学今年计划再购买文学书和科普书共200本,且购买文学书和科普书的总费用不超过2135元,这所中学今年至少要购买多少本文学书?
查看答案和解析>>
科目: 来源: 题型:
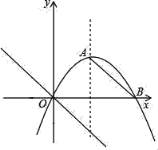
【题目】如图,抛物线y=ax2+2x与x轴相交于点B,其对称轴为x=3.
(1)求直线AB的解析式;
(2)过点O作直线l,使l∥AB,点P是l上一动点,设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为t,当0<S≤18时,求t的取值范围;
(3)在(2)的条件下,当t取最大值时,抛物线上是否存在点Q,使△OPQ为直角三角形且OP为直角边,若存在,求出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
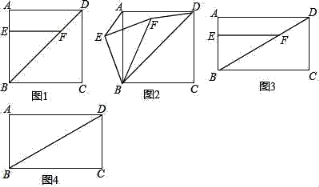
【题目】在四边形ABCD中,点E为AB边上的一点,点F为对角线BD上的一点,且EF⊥AB.
(1)若四边形ABCD为正方形.
①如图1,请直接写出AE与DF的数量关系 ;
②将△EBF绕点B逆时针旋转到图2所示的位置,连接AE,DF,猜想AE与DF的数量关系并说明理由.
(2)若四边形ABCD为矩形,BC=mAB,其他条件都不变.
①如图3,猜想AE与DF的数量关系并说明理由;
②将△EBF绕点B顺时针旋转α(0°<α<90°)得到△E′BF′,连接AE′,DF′,请在图4中画出草图,并直接写出AE′和DF′的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com