
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx+n经过点A(3,0)、
B(0,-3),点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横
坐标为t.
(1)分别求出直线AB和这条抛物线的解析式.
(2)若点P在第四象限,连接AM、BM,当线段PM最长时,求△ABM的面积.
(3)是否存在这样的点P,使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
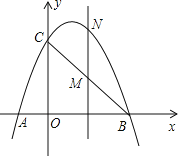
【题目】如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,3)三点。
(1)求抛物线的解析式。
(2)点M是线段BC上的点(不与B,C重合),过M作MN∥y轴交抛物线于N若点M的横坐标为m,请用m的代数式表示MN的长。
(3)在(2)的条件下,连接NB、NC,是否存在m,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面的材料:
∵![]() =
=![]() ×
×![]() ,
,![]() =
=![]() ×
×![]() ,
,![]() =
=![]() ×
×![]() ,…,
,…,![]() =
=![]() ×
×![]() ,
,
∴![]() +
+![]() +
+![]() +…+
+…+![]() =
=![]() ×
×![]() +
+![]() ×
×![]() +
+![]() ×
×![]() +…+
+…+![]() ×
×![]()
=![]() ×
×![]() =
=![]() ×
×![]() =
=![]() .
.
请解答下列问题:
(1)在和式![]() +
+![]() +
+![]() +…中,第100项是 ;
+…中,第100项是 ;
(2)化简![]() +
+![]() +
+![]() +…+
+…+![]() ,并求n=100时分式的值;
,并求n=100时分式的值;
(3)根据上面的方法,解方程:![]() +
+![]() +
+![]() =
=![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】小张去文具店购买作业本,作业本有大、小两种规格,大本作业本的单价比小本作业本贵0.3元,已知用8元购买大本作业本的数量与用5元购买小本作业本的数量相同.
(1)求大本作业本与小本作业本每本各多少元?
(2)因作业需要,小张要再购买一些作业本,购买小本作业本的数量是大本作业本数量的2倍,总费用不超过15元.则大本作业本最多能购买多少本?
查看答案和解析>>
科目: 来源: 题型:
【题目】我校课外兴趣活动小组深入农村,对某水稻品种的稻穗谷粒数目进行调查,从试验田中随机抽取了30株.
(1)对抽取的30株水稻稻穗谷粒数进行统计分析,请补全下表中空格,并完善直方图:

(2)如图所示的扇形统计图中,扇形A对应的圆心角为 度;

(3)该试验田中大约有3000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 中,如果过项点
中,如果过项点![]() 的一条直线把这个三角形分割成两个三角形,其中一个为等腰三角形,另一个为直角三角形,则称这条直线为
的一条直线把这个三角形分割成两个三角形,其中一个为等腰三角形,另一个为直角三角形,则称这条直线为![]() 的关于点
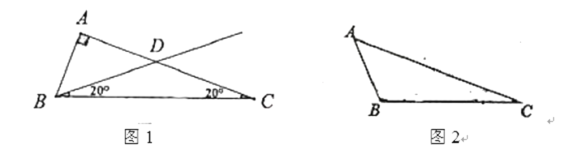
的关于点![]() 的二分割线.例如:如图1,
的二分割线.例如:如图1,![]() 中,
中,![]() ,
,![]() ,若过顶点
,若过顶点![]() 的一条直线
的一条直线![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,显然直线
,显然直线![]() 是
是![]() 的关于点
的关于点![]() 的二分割线.
的二分割线.
(1)在图2的![]() 中,
中,![]() ,
,![]() .请在图2中画出
.请在图2中画出![]() 关于点
关于点![]() 的二分割线,且
的二分割线,且![]() 角度是 ;
角度是 ;
(2)已知![]() ,在图3中画出不同于图1,图2的
,在图3中画出不同于图1,图2的![]() ,所画
,所画![]() 同时满足:①
同时满足:①![]() 为最小角;②存在关于点
为最小角;②存在关于点![]() 的二分割线.
的二分割线.![]() 的度数是 ;
的度数是 ;
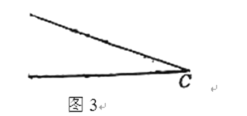
(3)已知![]() ,
,![]() 同时满足:①
同时满足:①![]() 为最小角;②存在关于点
为最小角;②存在关于点![]() 的二分割线.请求出
的二分割线.请求出![]() 的度数(用
的度数(用![]() 表示).
表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点C为线段AB上一点,分别以AB、AC、CB为底作顶角为120°的等腰三角形,顶角顶点分别为D、E、F(点E、F在AB的同侧,点D在另一侧)
(1)如图1,若点C是AB的中点,则∠AED= ;
(2)如图2,若点C不是AB的中点
①求证:△DEF为等边三角形;
②连接CD,若∠ADC=90°,AB=3,请直接写出EF的长.

查看答案和解析>>
科目: 来源: 题型:
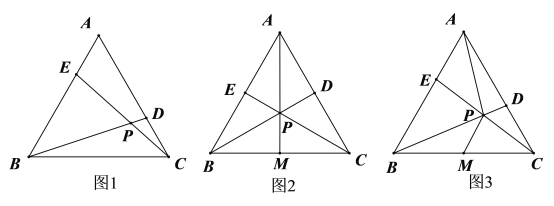
【题目】如图,在等边![]() 中,点
中,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的动点,且
上的动点,且![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)如图1,求证![]() ;
;
(2)点![]() 是边
是边![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
①如图2,若点![]() ,
,![]() ,
,![]() 三点共线,则
三点共线,则![]() 与
与![]() 的数量关系是 ;
的数量关系是 ;
②若点![]() ,
,![]() ,
,![]() 三点不共线,如图3,问①中的结论还成立吗?若成立,请给出证明,若不成立,请说明理由.
三点不共线,如图3,问①中的结论还成立吗?若成立,请给出证明,若不成立,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com