
科目: 来源: 题型:
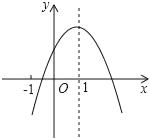
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:①abc<0;②b<a﹣c;③4a+2b+c>0;④2c<3b;⑤a+b<m(am+b),(m≠1的实数)⑥2a+b+c>0,其中正确的结论的有( )
A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目: 来源: 题型:
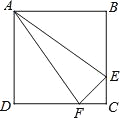
【题目】如图,正方形ABCD中,AB=4cm,点E、F同时从C点出发,以1cm/s的速度分别沿CB﹣BA、CD﹣DA运动,到点A时停止运动.设运动时间为t(s),△AEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
A. 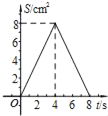 B.
B. 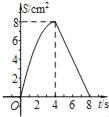
C. 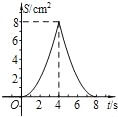 D.
D. 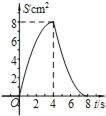
查看答案和解析>>
科目: 来源: 题型:
【题目】如图(1),已知小正方形![]() 的面积为1,把它的各边延长一倍得新正方形
的面积为1,把它的各边延长一倍得新正方形![]() ;把正方形
;把正方形![]() 边长按原法延长一倍得到正方形
边长按原法延长一倍得到正方形![]() 如图(2);以此下去,则正方形
如图(2);以此下去,则正方形![]() 的面积为_________________.
的面积为_________________.

查看答案和解析>>
科目: 来源: 题型:
【题目】某县冬季流感严重,学生感染较多,造成不少学校放假,为了预防流感,县教体局要求各校进行防控.某学校计划利用周末将教室及公共环境进行“喷药消毒”,现有甲、乙两位老师主动承接该工作,若甲、乙两老师合作6小时可以完成全部工作;若甲老师单独做4小时后,剩下的乙老师单独做还需9小时完成.求甲、乙两老师单独完成该工作各需多少小时?
查看答案和解析>>
科目: 来源: 题型:
【题目】(阅读材料)
对于二次三项式![]() 可以直接分解为
可以直接分解为![]() 的形式,但对于二次三项式
的形式,但对于二次三项式![]() ,就不能直接用公式了,我们可以在二次三项式
,就不能直接用公式了,我们可以在二次三项式![]() 中先加上一项
中先加上一项![]() ,使其成为完全平方式,再减去
,使其成为完全平方式,再减去![]() 这项,(这里也可把
这项,(这里也可把![]() 拆成
拆成![]() 与
与![]() 的和),使整个式子的值不变.
的和),使整个式子的值不变.
于是有:![]()
![]()
![]()
![]()
![]()
![]() ,
,
我们把像这样将二次三项式分解因式的方法叫做添(拆)项法.
(应用材料)
![]() 上式中添(拆)项后先把完全平方式组合在一起,然后用______法实现分解因式.
上式中添(拆)项后先把完全平方式组合在一起,然后用______法实现分解因式.
![]() 请你根据材料中提供的因式分解的方法,将下面的多项式分解因式:
请你根据材料中提供的因式分解的方法,将下面的多项式分解因式:
![]() ;
;
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在学习完第十二章后,张老师让同学们独立完成课本56页第9题:“如图1,![]() ,
,![]() ,
,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.”
的长.”

(1)请你也独立完成这道题:
(2)待同学们完成这道题后,张老师又出示了一道题:
在课本原题其它条件不变的前提下,将![]() 所在直线旋转到
所在直线旋转到![]() 的外部(如图2),请你猜想
的外部(如图2),请你猜想![]() ,
,![]() ,
,![]() 三者之间的数量关系,直接写出结论:_______.(不需证明)
三者之间的数量关系,直接写出结论:_______.(不需证明)
(3)如图3,将(1)中的条件改为:在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 三点在同一条直线上,并且有∠BEC=∠ADC=∠BCA=
三点在同一条直线上,并且有∠BEC=∠ADC=∠BCA=![]() ,其中
,其中![]() 为任意钝角,那么(2)中你的猜想是否还成立?若成立,请证明;若不成立,请说明理由:
为任意钝角,那么(2)中你的猜想是否还成立?若成立,请证明;若不成立,请说明理由:
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]() ,以原点
,以原点![]() 为位似中心,将
为位似中心,将![]() 缩小,使变换后得到的
缩小,使变换后得到的![]() 与
与![]() 对应边的比为
对应边的比为![]() ,则线段
,则线段![]() 的中点
的中点![]() 变换后对应的点的坐标为( )
变换后对应的点的坐标为( )
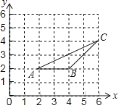
A. (2,![]() ) B. (-2,-
) B. (-2,-![]() ) C. (2,
) C. (2,![]() )或(-2,-
)或(-2,-![]() ) D. (8,6)或(-8,-6)
) D. (8,6)或(-8,-6)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,在平面直角坐标系中,二次函数y=﹣![]() x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
(1)填空:b= ,c= ;
(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;
(3)在x轴下方,该二次函数的图象上是否存在点M,使△PQM是以点P为直角顶点的等腰直角三角形?若存在,请求出运动时间t;若不存在,请说明理由;
(4)如图②,点N的坐标为(﹣![]() ,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.
,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“內似线”.
(1)等边三角形“內似线”的条数为 ;
(2)如图,△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求证:BD是△ABC的“內似线”;
(3)在Rt△ABC中,∠C=90°,AC=4,BC=3,E、F分别在边AC、BC上,且EF是△ABC的“內似线”,求EF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com