
科目: 来源: 题型:
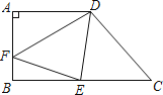
【题目】已知:如图,四边形ABCD中,AD∥BC,∠B=90°,AD=AB=4,BC=7,点E在BC上,将△CDE沿DE折叠,点C恰好落在AB边上的点F处.
(1)求线段DC的长度;
(2)求△FED的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E.
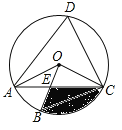
(1)求∠OCA的度数;
(2)若∠COB=3∠AOB,OC=![]() ,求图中阴影部分面积(结果保留π和根号).
,求图中阴影部分面积(结果保留π和根号).
查看答案和解析>>
科目: 来源: 题型:
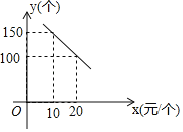
【题目】某旅游风景区出售一种纪念品,该纪念品的成本为![]() 元/个,这种纪念品的销售价格为
元/个,这种纪念品的销售价格为![]() (元/个)与每天的销售数量
(元/个)与每天的销售数量![]() (个)之间的函数关系如图所示.
(个)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)销售价格定为多少时,每天可以获得最大利润?并求出最大利润.
(3)“十一”期间,游客数量大幅增加,若按八折促销该纪念品,预计每天的销售数量可增加![]() ,为获得最大利润,“十一”假期该纪念品打八折后售价为多少?
,为获得最大利润,“十一”假期该纪念品打八折后售价为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两名战士在相同条件下各射击10次,每次命中的环数如下:
甲:8,6,7,8,9,10,6,5,4,7
乙:7,9,8,5,6,7,7,6,7,8
(1)分别计算以上两组数据的平均数;
(2)分别计算以上两组数据的方差.
查看答案和解析>>
科目: 来源: 题型:
【题目】创新需要每个人的参与,就拿小华来说,为了解决晒衣服的,聪明的他想到了一个好办法,在家宽敞的院内地面![]() 上立两根等长的立柱
上立两根等长的立柱![]() 、
、![]() (均与地面垂直),并在立柱之间悬挂一根绳子.由于挂的衣服比较多,绳子的形状近似成了抛物线
(均与地面垂直),并在立柱之间悬挂一根绳子.由于挂的衣服比较多,绳子的形状近似成了抛物线![]() ,如图
,如图![]() ,已知立柱
,已知立柱![]() 米,
米, ![]() 米.
米.
(1)求绳子最低点离地面的距离;
(2)为了防止衣服碰到地面,小华在离![]() 为
为![]() 米的位置处用一根垂直于地面的立柱
米的位置处用一根垂直于地面的立柱![]() 撑起绳子 (如图2),使左边抛物线
撑起绳子 (如图2),使左边抛物线![]() 的最低点距
的最低点距![]() 为
为![]() 米,离地面
米,离地面![]() 米,求
米,求![]() 的长.
的长.
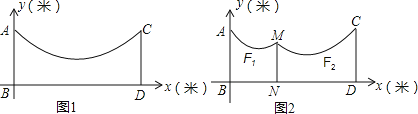
查看答案和解析>>
科目: 来源: 题型:
【题目】将两块全等的含30°角的直角三角板按图1的方式放置,已知∠BAC=∠B1A1C=30°,AB=2BC.
(1)固定三角板A1B1C,然后将三角板ABC绕点C顺时针方向旋转至图2的位置,AB与A1C、A1B1分别交于点D、E,AC与A1B1交于点F.
①填空:当旋转角等于20°时,∠BCB1= 度;
②当旋转角等于多少度时,AB与A1B1垂直?请说明理由.
(2)将图2中的三角板ABC绕点C顺时针方向旋转至图3的位置,使AB∥CB1,AB与A1C交于点D,试说明A1D=CD.

查看答案和解析>>
科目: 来源: 题型:
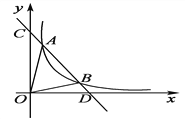
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出kx+b-![]() <0时x的取值范围;
<0时x的取值范围;
(3)求△AOB的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】合肥三十八中为预防秋季疾病传播,对教室进行“薰药消毒”.已知药物在燃烧释放过程中,室内空气中每立方米含药量![]() (毫克)与燃烧时间
(毫克)与燃烧时间![]() (分钟)之间的关系如图所示(即图中线段
(分钟)之间的关系如图所示(即图中线段![]() 和双曲线在
和双曲线在![]() 点及其右侧的部分),根据图象所示信息,解答下列问题:
点及其右侧的部分),根据图象所示信息,解答下列问题:
(1)写出从药物释放开始,![]() 与
与![]() 之间的函数关系式及自变量的取值范围;
之间的函数关系式及自变量的取值范围;
(2)据测定,只有当空气中每立方米的含药量不低于![]() 毫克时,对预防才有作用,且至少持续作用
毫克时,对预防才有作用,且至少持续作用![]() 分钟以上,才能完全杀死这种病毒,请问这次消毒是否彻底?
分钟以上,才能完全杀死这种病毒,请问这次消毒是否彻底?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y= ![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
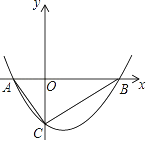
(1)求抛物线的解析式;
(2)判断△ABC的形状,证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com