
科目: 来源: 题型:
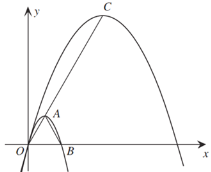
【题目】如图,抛物线C1:![]() 的顶点为A,与x轴的正半轴交于点B.
的顶点为A,与x轴的正半轴交于点B.
(1)请直接写出A、B两点的坐标,A ,B .
(2)将抛物线C1上的点的横坐标和纵坐标都扩大到原来的2倍,求变换后得到的抛物线的解析式;
(3)将抛物线C1上的点(x,y)变为(kx,ky)(|k|>1),变换后得到的抛物线记作C2.抛物线C2的顶点为C,点P在抛物线C2上,满足S△PAC=S△ABC,且∠ACP=90°.
①当k>1时,求k的值;
②当k<-1时,请你直接写出k的值,不必说明理由.
查看答案和解析>>
科目: 来源: 题型:
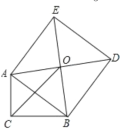
【题目】已知在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=4![]() ,OC=7,则另一条直角边BC的长为_____.
,OC=7,则另一条直角边BC的长为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如果方程x2+px+q=0的两个根是x1、x2,那么x1+x2=-p,x1·x2=q.请根据以上结论,解决下列问题:
(1)已知关于x的方程x2+mx+n=0 (n≠0),求出一个一元二次方程,使它的两根分别是已知方程两根的倒数;
(2)已知a、b满足a2-15a-5=0,b2-15b-5=0,求![]() 的值;
的值;
(3)已知a、b、c均为实数,且a+b+c=0,abc=16,求正数c的最小值.
查看答案和解析>>
科目: 来源: 题型:
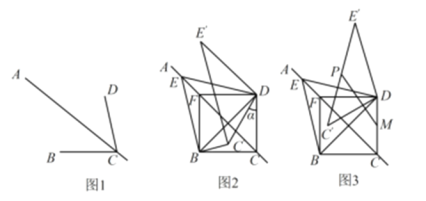
【题目】如图1,已知线段BC=2,点B关于直线AC的对称点是点D,点E为射线CA上一点,且ED=BD,连接DE,BE.
(1)依据题意补全图1,并证明:△BDE为等边三角形;
(2)若∠ACB=45°,点C关于直线BD的对称点为点F,连接FD、FB,将△CDE绕点D顺时针旋转![]() 度(0°<
度(0°<![]() <360°)得
<360°)得![]() , 点E的对应点为E’,点C的对应点为点C’.
, 点E的对应点为E’,点C的对应点为点C’.
(i)如图2,当![]() 时 ,连接BC’.证明:EF=BC’;
时 ,连接BC’.证明:EF=BC’;
(ii)如图3,点M为DC中点,点P为线段C’E’上任意一点,试探究:在此旋转过程中,线段PM长度的取值范围?(直接写出答案).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)求证:无论m取何值,原方程总有两个不相等的实数根;
(2)若x1,x2是原方程的两根,且![]() ,求m的值,并求出此时方程的两根.
,求m的值,并求出此时方程的两根.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】为落实“两免一补”政策,某市2011年投入教育经费2500万元,预计2013年要投入教育经费3600万元,已知2011年至2013年的教育经费投入以相同的百分率逐年增长,则2014年要投入的教育经费为多少万元?
查看答案和解析>>
科目: 来源: 题型:
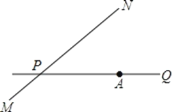
【题目】如图,公路 MN 和公路 PQ 在点 P 处交会,且∠QPN=30°.点 A 处有一所中学,AP=160m,一辆拖拉机从 P 沿公路 MN 前行,假设拖拉机行驶时周围 100m 以内会受到噪声影响,那么该所中学是否会受到噪声影响,请说明理由,若受影响,已知拖拉机的速度为 18km/h,那么学校受影响的时间为多长?
查看答案和解析>>
科目: 来源: 题型:
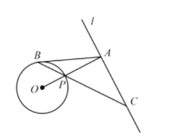
【题目】如图,已知直线l与⊙O 相离,OA⊥l于点A,交⊙O 于点P,点B是⊙O上一点,连接BP并延长,交直线l于点C,使得AB=AC.
(1)求证:AB是⊙O的切线;
(2)若PC=2![]() ,OA=3,求线段PB的长.
,OA=3,求线段PB的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人的某一人.
(1)求第二次传球后球回到甲手里的概率.
(2)如果甲跟另外n(n≥2)个人做(1)同样的游戏,那么,第三次传球后球回到甲手里的概率是 .(请用含n的式子直接写结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com