
科目: 来源: 题型:
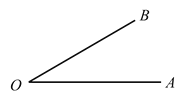
【题目】已知:∠AOB.
求作:∠A'O'B',使∠A'O'B'=∠AOB.
作法:①以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;
②画一条射线O'A',以点O'为圆心,OC长为半径面弧,交O'A'于点C;
③以点C'为圆心,CD长为半径画弧,与第②步中所画的弧相交于点D';
④过点D'画射线O'B’,则∠A'O'B'=∠AOB.
根据上面的作法,完成以下问题:
(1)使用直尺和圆规,作出∠A'O'B'(请保留作图痕迹).
(2)完成下面证明∠A'O'B'=∠AOB的过程(注:括号里填写推理的依据).
证明:由作法可知O'C'=OC,O'D'=OD,D'C'=_________,
∴△C'O'D'≌△COD(________)
∴∠A'O'B'=∠AOB(________)
查看答案和解析>>
科目: 来源: 题型:
【题目】某校举办校级篮球赛,进入决赛的队伍有A、B、C、D,要从中选出两队打一场比赛.
(1)若已确定A打第一场,再从其余三队中随机选取一队,求恰好选中D队的概率.
(2)请用画树状图或列表法,求恰好选中B、C两队进行比赛的概率
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在平面直角坐标系中,![]() ,
,![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 轴与点
轴与点![]() ,连接
,连接![]() ,
,![]() 为第一象限内的点.
为第一象限内的点.
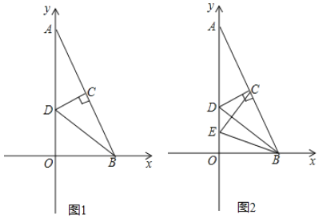
(1)求点![]() 坐标;
坐标;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)如图2,点![]() 为
为![]() 轴上的一个动点,当
轴上的一个动点,当![]() 为等腰三角形时,直接写出点
为等腰三角形时,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
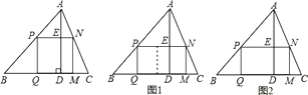
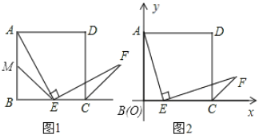
【题目】课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)加工成的正方形零件的边长是多少mm?
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少?请你计算.
(3)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
查看答案和解析>>
科目: 来源: 题型:
【题目】自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
累计车费 | 0 | 0.5 | 0.9 |
|
| 1.5 |
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 5 | 15 | 10 | 30 | 25 | 15 |
(Ⅰ)写出![]() 的值;
的值;
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利? 说明理由.
查看答案和解析>>
科目: 来源: 题型:
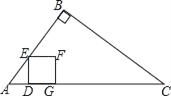
【题目】如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点D从点A出发以1cm/s的速度运动到点C停止.作DE⊥AC交边AB或BC于点E,以DE为边向右作正方形DEFG.设点D的运动时间为t(s).
(1)求AC的长.
(2)请用含t的代数式表示线段DE的长.
(3)当点F在边BC上时,求t的值.
(4)设正方形DEFG与△ABC重叠部分图形的面积为S(cm2),当重叠部分图形为四边形时,求S与t之间的函数关系式.
查看答案和解析>>
科目: 来源: 题型:
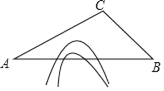
【题目】随着中国经济的快速发展以及科技水平的飞速提高,中国高铁正迅速崛起.高铁大大缩短了时空距离,改变了人们的出行方式.如图,A,B两地被大山阻隔,由A地到B地需要绕行C地,若打通穿山隧道,建成A,B两地的直达高铁,可以缩短从A地到B地的路程.已知:∠CAB=30°,∠CBA=45°,AC=640公里,求隧道打通后与打通前相比,从A地到B地的路程将约缩短多少公里?(参考数据:![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目: 来源: 题型:
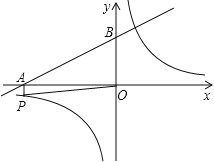
【题目】如图,已知反比例函数![]() (m是常数,m≠0),一次函数y=ax+b(a、b为常数,a≠0),其中一次函数与x轴,y轴的交点分别是A(-4,0),B(0,2).
(m是常数,m≠0),一次函数y=ax+b(a、b为常数,a≠0),其中一次函数与x轴,y轴的交点分别是A(-4,0),B(0,2).
(1)求一次函数的关系式;
(2)反比例函数图象上有一点P满足:①PA⊥x轴;②PO=![]() (O为坐标原点),求反比例函数的关系式;
(O为坐标原点),求反比例函数的关系式;
(3)求点P关于原点的对称点Q的坐标,判断点Q是否在该反比例函数的图象上.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,已知正方形![]() 的边长为1,点
的边长为1,点![]() 在边
在边![]() 上,若
上,若![]() ,且
,且![]() 交正方形外角的平分线
交正方形外角的平分线![]() 于点
于点![]() .
.
(1)如图1,若点![]() 是边
是边![]() 的中点,
的中点,![]() 是边
是边![]() 的中点,连接
的中点,连接![]() ,求证:
,求证:![]() .
.
(2)如图2,若点![]() 在线段
在线段![]() 上滑动(不与点
上滑动(不与点![]() ,
,![]() 重合).
重合).
①在点![]() 滑动过程中,
滑动过程中,![]() 是否一定成立?请说明理由;
是否一定成立?请说明理由;
②在如图所示的直角坐标系中,当点![]() 滑动到某处时,点
滑动到某处时,点![]() 恰好落在直线
恰好落在直线![]() 上,求此时点
上,求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】小慧根据学习函数的经验,对函数![]() 的图像与性质进行了探究.下面是小慧的探究过程,请补充完整.
的图像与性质进行了探究.下面是小慧的探究过程,请补充完整.
(l)函数![]() 的自变量
的自变量![]() 的取值范围是 ;
的取值范围是 ;
(2)列表,找出![]() 与
与![]() 的几组对应值.
的几组对应值.

其中,![]() ;
;
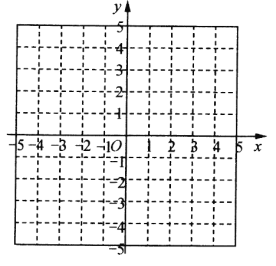
(3)在平面直角坐标系![]() 中,描出以上表中各对对应值为坐标的点,并画出该函数的图像;
中,描出以上表中各对对应值为坐标的点,并画出该函数的图像;
(4)写出该函数的一条性质: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com