
科目: 来源: 题型:
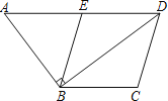
【题目】如图,四边形ABCD中,AD∥BC,AD=2BC,E为AD的中点,∠ABD=90°.
(1)求证:四边形BCDE是菱形;
(2)连接CE,若CE=6,BC=5,求四边形ABCD的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,为测量某建筑物AB的高度,在离该建筑物底部20m的点C处,目测建筑物顶端A处,视线与水平线夹角∠ADE为38.5°,目高CD为1.6m.求建筑物AB的高度.(结果精确到1m)(参考数据:sin38.5°=0.623,cos38.5°=0.783,tan38.5°=0.795)

查看答案和解析>>
科目: 来源: 题型:
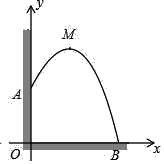
【题目】从某幢建筑物10m高的窗口A处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与地面垂直).抛物线的最高点M离墙1m,离地面![]() m.
m.
(1)建立适当的平面直角坐标系,求抛物线的解析式.
(2)求水的落地点B与点O的距离.
查看答案和解析>>
科目: 来源: 题型:
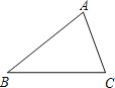
【题目】下面是小芸设计的“作三角形一边上的中线”的尺规作图过程.
已知:△ABC.
求作:BC边上的中线AD.
作法:
(1)分别以点B,C为圆心,AC,AB长为半径画弧,
两弧相交于P点;
(2)作直线AP,AP与BC交于D点.
线段AD就是所求作的BC边上的中线.
根据小芸设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:连接BP,CP,
∵AB=CP,AC=______,
∴四边形ABPC是平行四边形,(______)(填推理的依据)
∴BD=DC,(______)(填推理的依据)
即线段AD是BC边上的中线.
查看答案和解析>>
科目: 来源: 题型:
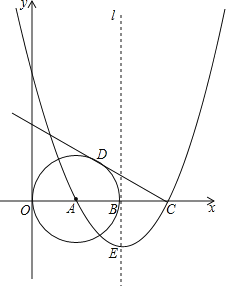
【题目】如图,已知点A(2,0),以A为圆心作⊙A与y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.
(1)以直线l为对称轴的抛物线过点A,抛物线与x轴的另一个交点为点C,抛物线的顶点为点E,如果CO=2BE,求此抛物线的解析式;
(2)过点C作⊙A的切线CD,D为切点,求此切线长;
(3)点F是切线CD上的一个动点,当△BFC与△CAD相似时,求出BF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,∠BAC的角平分线AE交⊙O于点E,交BC于点D,过点E作直线l∥BC.
(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若在AE上取一点F使EF=BE,求证:BF是∠ABC的平分线;
(3)在(2)的条件下,若DE=3,BE=5,求AE的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是斜边
是斜边![]() 的中点.点
的中点.点![]() 从点
从点![]() 出发以
出发以![]() 的速度向点
的速度向点![]() 运动,点
运动,点![]() 同时从点
同时从点![]() 出发以一定的速度沿射线
出发以一定的速度沿射线![]() 方向运动,规定当点
方向运动,规定当点![]() 到终点
到终点![]() 时停止运动.设运动的时间为
时停止运动.设运动的时间为![]() 秒,连接
秒,连接![]() 、
、![]() .
.
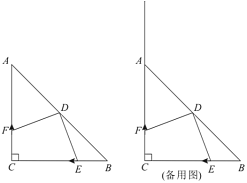
(1)填空:![]() ______
______![]() ;
;
(2)当![]() 且点
且点![]() 运动的速度也是
运动的速度也是![]() 时,求证:
时,求证:![]() ;
;
(3)若动点![]() 以
以![]() 的速度沿射线
的速度沿射线![]() 方向运动,在点
方向运动,在点![]() 、点
、点![]() 运动过程中,如果存在某个时间
运动过程中,如果存在某个时间![]() ,使得
,使得![]() 的面积是
的面积是![]() 面积的两倍,请你求出时间
面积的两倍,请你求出时间![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
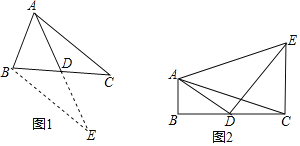
【题目】数学兴趣小组在活动时,老师提出了这样一个问题:如图1,在![]() 中,
中,![]() ,
,![]() ,D是BC的中点,求BC边上的中线AD的取值范围.
,D是BC的中点,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使![]() ,请补充完整证明“
,请补充完整证明“![]() ≌
≌![]() ”的推理过程.
”的推理过程.
![]() 求证:
求证:![]() ≌
≌![]()
证明:![]() 延长AD到点E,使
延长AD到点E,使![]()
在![]() 和
和![]() 中
中![]() 已作
已作![]() ,
,
![]() ______
______![]() ,
,
![]() 中点定义
中点定义![]() ,
,
![]() ≌
≌![]() ______
______![]() ,
,
![]() 探究得出AD的取值范围是______;
探究得出AD的取值范围是______;
(感悟)解题时,条件中若出现“中点”“中线”等字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
(问题解决)
![]() 如图2,
如图2,![]() 中,
中,![]() ,
,![]() ,AD是
,AD是![]() 的中线,
的中线,![]() ,
,![]() ,且
,且![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com