
科目: 来源: 题型:
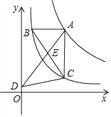
【题目】如图,点A是反比例函数y=![]() 图象上的任意一点,过点A作AB∥x轴,AC∥y轴,分别交反比例函数y=
图象上的任意一点,过点A作AB∥x轴,AC∥y轴,分别交反比例函数y=![]() 的图象于点B,C,连接BC,E是BC上一点,连接并延长AE交y轴于点D,连接CD,则S△DEC﹣S△BEA=_________.
的图象于点B,C,连接BC,E是BC上一点,连接并延长AE交y轴于点D,连接CD,则S△DEC﹣S△BEA=_________.
查看答案和解析>>
科目: 来源: 题型:
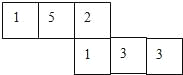
【题目】标有 6 个数字的立方体的表面展开图如图所示,掷这个立方体一次,记朝上一面的数为 x,朝下一面的数字为 y,得到平面直角坐标中的一个点(x,y),小敏抛掷一次立方体,则所得的点落在以坐标系原点为圆心,3 为半径的圆内的概率为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标(1,n)与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②-1≤a≤-![]() ;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n-1有两个不相等的实数根.其中结论正确的个数为( )
;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n-1有两个不相等的实数根.其中结论正确的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,∠C=90°、AD是角平分线,E为AC边上的点,DE=DB,下列结论:①∠DEA+∠B=180°;② ∠CDE=∠CAB;③ AC=![]() (AB+AE);④ S△ADC=
(AB+AE);④ S△ADC=![]() S四边形ABDE,其中正确的结论个数为( )
S四边形ABDE,其中正确的结论个数为( )
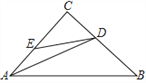
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线c:y=x2+2x﹣3,将抛物线c平移得到抛物线c′,如果两条抛物线,关于直线x=1对称,那么下列说法正确的是( )
A. 将抛物线c沿x轴向右平移![]() 个单位得到抛物线c′ B. 将抛物线c沿x轴向右平移4个单位得到抛物线c′
个单位得到抛物线c′ B. 将抛物线c沿x轴向右平移4个单位得到抛物线c′
C. 将抛物线c沿x轴向右平移![]() 个单位得到抛物线c′ D. 将抛物线c沿x轴向右平移6个单位得到抛物线c′
个单位得到抛物线c′ D. 将抛物线c沿x轴向右平移6个单位得到抛物线c′
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:一个自然数,右边的数字总比左边的数字小,我们称它为“下滑数”(如:32,641,8531等).现从两位数中任取一个,恰好是“下滑数”的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
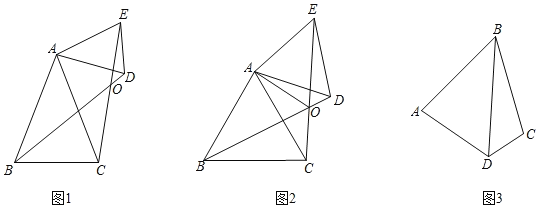
【题目】(阅读材科)小明同学发现这样一个规律:两个顶角相等的等腰三角形,
如果具有公共的项角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小明发现若∠BAC=∠DAE,AB=AC,AD=AE,则△ABD≌△ACE.
(材料理解)(1)在图1中证明小明的发现.
(深入探究)(2)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:①BD=EC;②∠BOC=60°;③∠AOE=60°;④EO=CO,其中正确的有 .(将所有正确的序号填在横线上).
(延伸应用)(3)如图3,AB=BC,∠ABC=∠BDC=60°,试探究∠A与∠C的数量关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】中国派遣三艘海监船在南海保护中国渔民不受菲律宾的侵犯.在雷达显示图上,标明了三艘海监船的坐标为![]() 、
、![]() 、
、![]() ,(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为
,(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为![]() 的圆形区域(只考虑在海平面上的探测).
的圆形区域(只考虑在海平面上的探测).
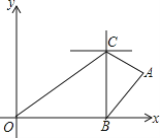
(1)若在三艘海监船组成的![]() 区域内没有探测盲点,则雷达的有效探测半径
区域内没有探测盲点,则雷达的有效探测半径![]() 至少为________海里;
至少为________海里;
(2)某时刻海面上出现一艘菲律宾海警船![]() ,在海监船
,在海监船![]() 测得点
测得点![]() 位于南偏东
位于南偏东![]() 方向上,同时在海监船
方向上,同时在海监船![]() 测得
测得![]() 位于北偏东
位于北偏东![]() 方向上,海警船
方向上,海警船![]() 正以每小时
正以每小时![]() 海里的速度向正西方向移动,我海监船
海里的速度向正西方向移动,我海监船![]() 立刻向北偏东
立刻向北偏东![]() 方向运动进行拦截,问我海监船
方向运动进行拦截,问我海监船![]() 至少以多少速度才能在此方向上拦截到菲律宾海警船
至少以多少速度才能在此方向上拦截到菲律宾海警船![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com