
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数 y=nx+2(n≠0)的图像与反比例函数 y ![]() (m≠0)在第一象限内的图像交于点 A,与 x 轴交于点 B,线段 OA=5,C 为 x 轴正半轴上一点,且 sin AOC
(m≠0)在第一象限内的图像交于点 A,与 x 轴交于点 B,线段 OA=5,C 为 x 轴正半轴上一点,且 sin AOC ![]() .
.
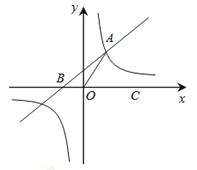
(1)求一次函数和反比例函数的解析式;
(2)求△ AOB 的面积;
(3)请直接写出不等式 nx 2 ![]() 的解.
的解.
查看答案和解析>>
科目: 来源: 题型:
【题目】曲阜限制“三小车辆”出行后,为方便市民出行,准备为![]() 、
、![]() 、
、![]() 、
、![]() 四个村建一个公交车站
四个村建一个公交车站![]() .
.
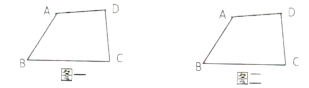
(1)请问:公交站![]() 建在何处才能使它到4个村的距离之和
建在何处才能使它到4个村的距离之和![]() 最小,请在图一中找出点
最小,请在图一中找出点![]() ;
;
(2)请问:公交站![]() 建在何处才能使它到道路
建在何处才能使它到道路![]() 、
、![]() 、
、![]() 的距离相等,请在图二中找出点
的距离相等,请在图二中找出点![]() 并加以说明.
并加以说明.
查看答案和解析>>
科目: 来源: 题型:
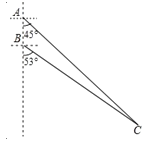
【题目】如图所示,我国两艘海监船 A,B 在南海海域巡逻,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船 C,此时,B 船在A 船的正南方向 15 海里处,A 船测得渔船 C 在其南偏东 45°方向,B 船测得渔船 C 在其南偏东 53°方向,已知 A 船的航速为 30 海里/小时,B 船的航速为 25 海里/小时,问 C 船至少要等待多长时间才能得到救援?(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈ 4 ,
,tan53°≈ 4 ,![]() 1.41 )
1.41 )
查看答案和解析>>
科目: 来源: 题型:
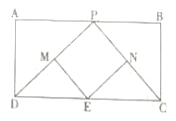
【题目】如图,已知矩形![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上一动点,
上一动点,![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点.
的中点.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)当![]() 为何值时,四边形
为何值时,四边形![]() 是菱形,说明理由.
是菱形,说明理由.
(3)四边形![]() 有可能是矩形吗?若有可能,求出
有可能是矩形吗?若有可能,求出![]() 的长;若不可能,请说明理由.
的长;若不可能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,△ ABC 在直角坐标系内,三个顶点的坐标分别为A(-2,2)、B(-1,0)、C(0,1)(正方形网格中每个小正方形的边长是一个单位长度).
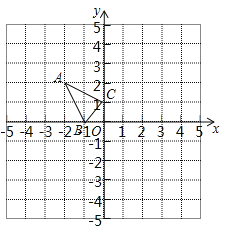
(1)画出△ ABC 关于 y 轴的轴对称图形△ A1B1C1;
(2)一点 O 为位拟中心,在网格内画出所有符合条件的△ A2B2C2,使△ A2B2C2 与△ A1B1C1 位拟,且位拟比为 2:1;
(3) △ A1B1C1 与△ A2B2C2 的面积比为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:直线y=ax+b与直线y=bx+a互为“友好直线”.如:直线y=2x+1与直线y=x+2互为“友好直线”.
(1)点M(m,2)在直线y=-x+4的“友好直线”上,则m=________;
(2)直线y=4x+3上的一点M(m,n)又是它的“友好直线”上的点,求点M的坐标;
(3)对于直线y=ax+b上的任意一点M(m,n),都有点N(2m,m-2n)在它的“友好直线”上,求直线y=ax+b的解析式.
查看答案和解析>>
科目: 来源: 题型:
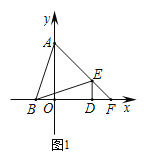
【题目】如图1,在平面直角坐标系中,点A(0,3),点B(-1,0),点D(2,0),DE⊥x轴且∠BED=∠ABD,延长AE交x轴于点F.
(1)求证:∠BAE=∠BEA;
(2)求点F的坐标;
(3)如图2,若点Q(m,-1)在第四象限,点M在y轴的正半轴上,∠MEQ=∠OAF,设AM-MQ=n,求m与n的数量关系,并证明.
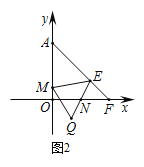
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料,完成(1)-(3)题.
数学课上,老师出示了这样一道题:
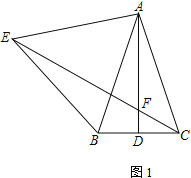
如图1,已知等腰△ABC中,AB=AC,AD为BC边上的中线,以AB为边向AB左侧作等边△ABE,直线CE与直线AD交于点F.请探究线段EF、AF、DF之间的数量关系,并证明.
同学们经过思考后,交流了自已的想法:
小明:“通过观察和度量,发现∠DFC的度数可以求出来.”
小强:“通过观察和度量,发现线段DF和CF之间存在某种数量关系.”
小伟:“通过做辅助线构造全等三角形,就可以将问题解决.”
......
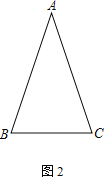
老师:“若以AB为边向AB右侧作等边△ABE,其它条件均不改变,请在图2中补全图形,探究线段EF、AF、DF三者的数量关系,并证明你的结论.”
(1)求∠DFC的度数;
(2)在图1中探究线段EF、AF、DF之间的数量关系,并证明;
(3)在图2中补全图形,探究线段EF、AF、DF之间的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com