
科目: 来源: 题型:
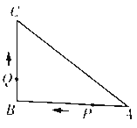
【题目】如图,已知△ABC中,∠B=90°,AB=8 cm,BC=6 cm,P,Q是△ABC边上的两个动点,点P从点A开始沿A→B方向运动,且速度为1 cm,点Q从点B开始沿B→C方向运动,且速度为2 cm/s,它们同时出发,设运动的时间为t s.
(1)运动几秒时,△APC是等腰三角形?
(2)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
查看答案和解析>>
科目: 来源: 题型:
【题目】某玩具店进了一排黑白塑料球,共5箱,每箱的规格、数量都相同,其中每箱中装有黑白两种颜色的塑料球共3000个,为了估计每箱中两种颜色球的个数,随机抽查了一箱,将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,发现摸到黑球的概率在0.8附近波动,则此可以估计这批塑料球中黑球的总个数,请将黑球总个数用科学记数法表示约为________个.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 均为整数),则有
均为整数),则有![]() .
.
∴![]() .这样小明就找到了一种把部分
.这样小明就找到了一种把部分![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
当![]() 均为正整数时,若
均为正整数时,若![]() ,用含m、n的式子分别表示
,用含m、n的式子分别表示![]() ,得
,得![]() = ,
= ,![]() = ;
= ;
(2)利用所探索的结论,找一组正整数![]() ,填空: + =( +
,填空: + =( + ![]() )2;
)2;
(3)若![]() ,且
,且![]() 均为正整数,求
均为正整数,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列三个判断中:①当x>0时,y>0;②若a=﹣1,则b=4;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;正确的是( )
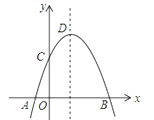
A. ① B. ② C. ③ D. ①②③都不对
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最
短距离为 ▲ cm.

查看答案和解析>>
科目: 来源: 题型:
【题目】一个盒子里有完全相同的三个小球,球上分别标上数字-1、1、2.随机摸出一个小球(不放回),其数字记为p,再随机摸出另一个小球,其数字记为q,则p,q使关于x的方程x2+px+q=0有实数根的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在一个不透明的布袋中装有相同的三个小球,其上面分别标注数字1、2、3、,现从中任意摸出一个小球,将其上面的数字作为点M的横坐标;将球放回袋中搅匀,再从中任意摸出一个小球,将其上面的数字作为点M的纵坐标.
(1)求点M在直线y=x上的概率;
(2)求点M的横坐标与纵坐标之和是偶数的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校九年级举行毕业典礼,需要从九年(1)班的2名男生1名女生(男生用A1表示,女生用B1表示)和九年(2)班的1名男生1名女生(男生用A2表示,女生用B2表示)共5人中随机选出2名主持人.
(1)用树状图或列表法列出所有可能情形;
(2)求2名主持人来自不同班级的概率;
(3)求2名主持人恰好1男1女的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在一个不透明的口袋中装有3个带号码的球,球号分别为2,3,4,这些球除号码不同外其它均相同。甲、乙、两同学玩摸球游戏,游戏规则如下:
先由甲同学从中随机摸出一球,记下球号,并放回搅匀,再由乙同学从中随机摸出一球,记下球号。将甲同学摸出的球号作为一个两位数的十位上的数,乙同学的作为个位上的数。若该两位数能被4整除,则甲胜,否则乙胜.
问:这个游戏公平吗?请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com