
科目: 来源: 题型:
【题目】如图,![]() 分别表示两名同学沿着同一路线运动的一次函数图象,图中
分别表示两名同学沿着同一路线运动的一次函数图象,图中![]() 和
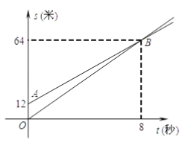
和![]() 分别表示运动路程和时间,已知甲的速度比乙快.有下列结论:
分别表示运动路程和时间,已知甲的速度比乙快.有下列结论:
①射线![]() 表示甲的运动路程与时间的函数关系
表示甲的运动路程与时间的函数关系
②甲出发时,乙已经在甲前面12米;
③8秒后,甲超过了乙;
④64秒时,甲追上了乙
其中,正确结论的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】几何学的产生,源于人们对土地面积测量的需要,以面积早就成为人们认识图形性质与几何证明的有效工具,可以说几何学从一开始便与面积结下了不解之缘.我们已经掌握了平行四边形面积的求法,但是一般四边形的面积往往不易求得,那么我们能否将其转化为平行四边形来求呢?
(1)方法1:如图①,连接四边形![]() 的对角线
的对角线![]() ,
,![]() ,分别过四边形
,分别过四边形![]() 的四个顶点作对角线的平行线,所作四条线相交形成四边形
的四个顶点作对角线的平行线,所作四条线相交形成四边形![]() ,易证四边形
,易证四边形![]() 是平行四边形.请直接写出S四边形ABCD和
是平行四边形.请直接写出S四边形ABCD和![]() 之间的关系:_______________.
之间的关系:_______________.
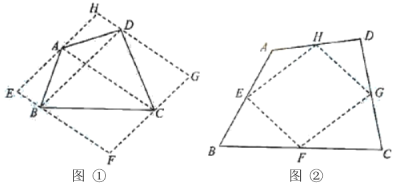
方法2:如图②,取四边形![]() 四边的中点
四边的中点![]() ,
,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() ,
,
(2)求证:四边形![]() 是平行四边形;
是平行四边形;
(3)请直接写出S四边形ABCD与![]() 之间的关系:_____________.
之间的关系:_____________.
方法3:如图③,取四边形![]() 四边的中点
四边的中点![]() ,
,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() 交于点
交于点![]() .先将四边形
.先将四边形![]() 绕点
绕点![]() 旋转
旋转![]() 得到四边形
得到四边形![]() ,易得点
,易得点![]() ,
,![]() ,
,![]() 在同一直线上;再将四边形
在同一直线上;再将四边形![]() 绕点
绕点![]() 旋转
旋转![]() 得到四边形
得到四边形![]() ,易得点
,易得点![]() ,
,![]() ,
,![]() 在同一直线上;最后将四边形
在同一直线上;最后将四边形![]() 沿
沿![]() 方向平移,使点
方向平移,使点![]() 与点
与点![]() 重合,得到四边形
重合,得到四边形![]() ;
;
(4)由旋转、平移可得![]() _________,
_________,![]() _________,所以
_________,所以![]() ,所以点
,所以点![]() ,
,![]() ,
,![]() 在同一直线上,同理,点
在同一直线上,同理,点![]() ,
,![]() ,
,![]() 也在同一点线上,所以我们拼接成的图形是一个四边形.
也在同一点线上,所以我们拼接成的图形是一个四边形.
(5)求证:四边形![]() 是平行四边形.
是平行四边形.

(注意:请考生在下面2题中任选一题作答如果多做,则按所做的第一题计分)
(6)应用1:如图④,在四边形![]() 中,对角线
中,对角线![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() ,则S四边形ABCD=
,则S四边形ABCD= ![]() .
.
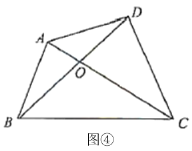
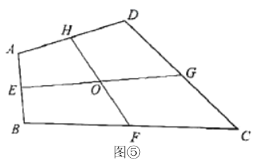
(7)应用2:如图⑤,在四边形![]() 中,点
中,点![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() ,则S四边形ABCD=___________
,则S四边形ABCD=___________![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校要从数学竞赛初赛成绩相同的四名学生(其中2名男生,2名女生)中,随机选出2名学生去参加决赛,则选出的2名学生恰好为1名男生和1名女生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】手机可以通过“个人热点”功能实现移动网络共享,小明和小亮准备到操场上测试个人热点连接的有效距离,他们从相距![]() 的
的![]() ,
,![]() 两地相向而行.图中
两地相向而行.图中![]() ,
,![]() 分别表示小明、小亮两人离
分别表示小明、小亮两人离![]() 地的距离
地的距离![]() 与步行时间
与步行时间![]() 之间的函数关系,其中
之间的函数关系,其中![]() 的关系式为
的关系式为![]() .根据图象回答下列问题:
.根据图象回答下列问题:

(1)请写出![]() 的关系式___________;
的关系式___________;
(2)小明和小亮出发后经过了多长时间相遇?
(3)如果手机个人热点连接的有效距离不超过![]() ,那么他们出发多长时间才能连接成功?连接持续了多长时间?
,那么他们出发多长时间才能连接成功?连接持续了多长时间?
查看答案和解析>>
科目: 来源: 题型:
【题目】某商店计划购进![]() ,
,![]() 两种型号的电机,其中每台
两种型号的电机,其中每台![]() 型电机的进价比
型电机的进价比![]() 型多
型多![]() 元,且用
元,且用![]() 元购进
元购进![]() 型电机的数量与用
型电机的数量与用![]() 元购进
元购进![]() 型电机的数量相等.
型电机的数量相等.
(1)求![]() ,
,![]() 两种型号电机的进价;
两种型号电机的进价;
(2)该商店打算用不超过![]() 元的资金购进
元的资金购进![]() ,
,![]() 两种型号的电机共
两种型号的电机共![]() 台,至少需要购进多少台
台,至少需要购进多少台![]() 型电机?
型电机?
查看答案和解析>>
科目: 来源: 题型:
【题目】一枚正方形骰子的六个面上分别标有1~6六个正整数,连续投掷这枚骰子两次,朝上的两个数依次作为一个点的横坐标、纵坐标,则这个点落在双曲线![]() 上的概率为( ).
上的概率为( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,梯形ABCD中,AB∥CD,AB=24cm,DC=10cm,点P和Q同时从D、B出发,P由D向C运动,速度为每秒1cm,点Q由B向A运动,速度为每秒3cm,试求几秒后,P、Q和梯形ABCD的两个顶点所形成的四边形是平行四边形?
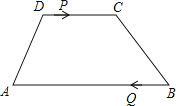
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,甲乙两个转盘被等分成五个扇形区域,上面分别标有数字,同时自由转动两个转盘,转盘停止后,连个指针同时落在偶数上的概率是( )
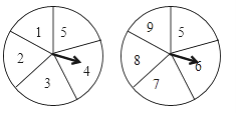
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】把八个完全相同的小球平分为两组,每组中每个分别写上1,2,3,4四个数字,然后分别装入不透明的口袋内搅匀,从第一个口袋内取出一个数记下数字后作为点P的横坐标x,然后再从第二个口袋中取出一个球记下数字后作为点P的纵坐标,则点P(x,y)落在直线y=﹣x+5上的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com