
科目: 来源: 题型:
【题目】某公司2017年初刚成立时投资1000万元购买新生产线生产新产品,此外,生产每件该产品还需要成本40元.按规定,该产品售价不得低于60元/件且不超过160元/件,且每年售价确定以后不再变化,该产品的年销售量![]() (万件)与产品售价
(万件)与产品售价![]() (元)之间的函数关系如图所示.
(元)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出
之间的函数关系式,并写出![]() 的取值范围;
的取值范围;
(2)求2017年该公司的最大利润?
(3)在2017年取得最大利润的前提下,2018年公司将重新确定产品售价,能否使两年共盈利达980万元.若能,求出2018年产品的售价;若不能,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图![]() ,直线
,直线![]() 是足球场的底线,
是足球场的底线,![]() 是球门,
是球门,![]() 点是射门点,连接
点是射门点,连接![]() ,
,![]() 叫做射门角.
叫做射门角.
(1)如图![]() ,点
,点![]() 是射门点,另一射门点
是射门点,另一射门点![]() 在过
在过![]() 三点的圆外(未超过底线
三点的圆外(未超过底线![]() ).证明:
).证明:![]()
(2)如图![]() ,
,![]() 经过球门端点
经过球门端点![]() ,直线
,直线![]() ,垂足为
,垂足为![]() 且与
且与![]() 相切与点
相切与点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,求此时一球员带球沿直线
,求此时一球员带球沿直线![]() 向底线方向运球时最大射门角的度数.
向底线方向运球时最大射门角的度数.
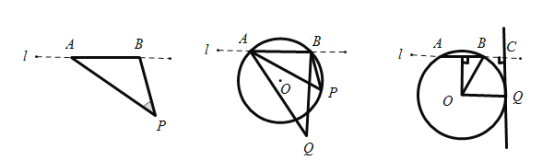
查看答案和解析>>
科目: 来源: 题型:
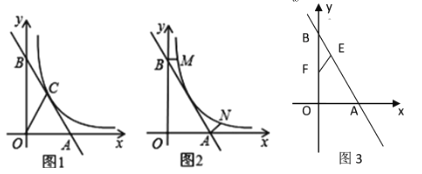
【题目】如图1,一次函数y=2x+4的图象交x轴于点A,交y轴于点B,与反比例函数y=![]() (x>0)的图象交于点C,连OC,若S△AOC=2.
(x>0)的图象交于点C,连OC,若S△AOC=2.
(1)求反比例函数的解析式;
(2)如图3,点E, F分别是线段AB和线段OB上的动点,点E从点B出发,沿线段BA运动,点F从点O出发,沿线段OB运动,速度都是每秒1个单位长度。运动时间为t秒,当其中一点到达终点后,另一点也随之停止运动.是否存在某个时刻。使得△BEF是直角三角形?若存在,求出t的值若不存在,请说明理由:
(3)如图2,过点B作BM⊥OB交反比例函数y=![]() (x>0)的图象于点M,点N为反比例函数 y=
(x>0)的图象于点M,点N为反比例函数 y=![]() (x>0)的图象上一点,∠ABM =∠BAN,求直线AN的解析式,
(x>0)的图象上一点,∠ABM =∠BAN,求直线AN的解析式,
查看答案和解析>>
科目: 来源: 题型:
【题目】一个四边形被一条对角线分割成两个三角形,如果被分割的两个三角形相似,我们把这条对角线称为该四边形的为相似对角线。
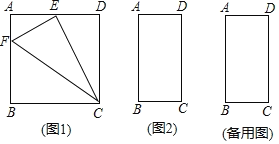
(1)如图1,正方形ABCD的边长为4,E为AD的中点,AF=1,连结CE,CF,求证:EF为四边形AECF的相似对角线。
(2)在四边形ABCD中,∠BAD=120°,AB=3,AC=![]() ,AC平分∠BAD,且AC是四边形ABCD的相似对角线,求BD的长。
,AC平分∠BAD,且AC是四边形ABCD的相似对角线,求BD的长。
(3)如图2,在矩形ABCD中,AB=6,BC=4,点E是线段AB(不取端点A,B)上的一个动点,点F是射线AD上的一个动点,若EF是四边形AECF的相似对角线,求BE的长.(直接写出答案)
查看答案和解析>>
科目: 来源: 题型:
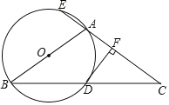
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
(1)试说明DF是⊙O的切线;
(2)若AC=3AE=6,求tanC
查看答案和解析>>
科目: 来源: 题型:
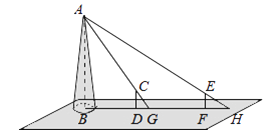
【题目】如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB,标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高.
查看答案和解析>>
科目: 来源: 题型:
【题目】某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y (℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?

查看答案和解析>>
科目: 来源: 题型:
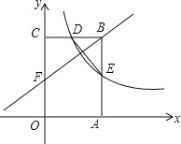
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3),反比例函数y=![]() (k>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(k>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)求反比例函数的表达式及点E的坐标;
(2)点F是OC边上一点,若△FBC∽△DEB,求点F的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com