
科目: 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线交于P.下面结论:
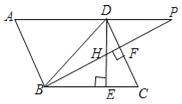
①![]() ,②∠A=∠BHE,③AB=BH,④△BHD∽△BDP.
,②∠A=∠BHE,③AB=BH,④△BHD∽△BDP.
请你把你认为正确的结论的番号都填上 (填错一个该题得0分)
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表所示.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
下列说法:①抛物线与y轴的交点为(0,6); ②抛物线的对称轴在y轴的右侧;③抛物线一定经过点(3,0);④在对称轴左侧,y随x增大而减小.⑤不等式ax2+(b﹣3)x+c﹣6>0解集为﹣2<x<0.其中说法正确的有( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点G,D,C在直线a上,点E,F,A,B在直线b上,若a∥b,Rt△GEF从如图所示的位置出发,沿直线b向右匀速运动,直到EG与BC重合.运动过程中△GEF与矩形ABCD重合部分的面积(S)随时间(t)变化的图象大致是( )

A.  B.
B.  C.
C. 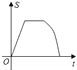 D.
D. 
查看答案和解析>>
科目: 来源: 题型:
【题目】将边长为3cm的正三角形的各边三等分,以这六个分点为顶点构成一个正六边形,再顺次连接这个正六边形的各边中点,又形成一个新的正六边形,则这个新的正六边形的面积等于( )
A. ![]() cm2 B.
cm2 B. ![]() cm2 C.
cm2 C. ![]() cm2 D.
cm2 D. ![]() cm2
cm2
查看答案和解析>>
科目: 来源: 题型:
【题目】我们把经过原点,顶点落在同一抛物线C上的所有抛物线称为抛物线C的派生抛物线.
(1)若y1=﹣x2+4x是抛物线C:y=ax2+2的派生抛物线,求a的值.
(2)证明:经过原点的抛物线y=﹣mx2+2mx+m﹣2是抛物线C:y=![]() x2+
x2+![]() 的派生抛物线;
的派生抛物线;
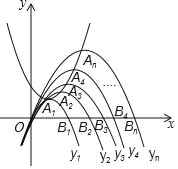
(3)如图,抛物线y1,y2,y3,y4…yn都是抛物线C:y=x2﹣2x+2的派生抛物线,其顶点A1,A2,A3,A4…An的横坐标分别是1、2、3、4…n,它们与x轴的另一个交点分别是B1,B2,B3,B4…Bn,与原点O构成的三角形分别为△OA1B1,△OA2B2,△OA3B3,△OA4B4…△OAnBn.
①请用含n的代数式表示抛物线yn的函数表达式;
②在这些三角形中,是否存在两个相似的三角形,若存在,请直接写出它们所对应的两个函数的表达式,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
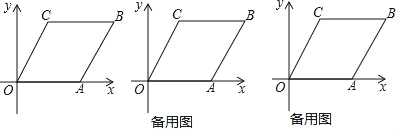
【题目】如图,在边长为5的菱形OABC中,sin∠AOC=![]() ,O为坐标原点,A点在x轴的正半轴上,B,C两点都在第一象限.点P以每秒1个单位的速度沿O→A→B→C→O运动一周,设运动时间为t(秒).请解答下列问题:
,O为坐标原点,A点在x轴的正半轴上,B,C两点都在第一象限.点P以每秒1个单位的速度沿O→A→B→C→O运动一周,设运动时间为t(秒).请解答下列问题:
(1)当CP⊥OA时,求t的值;
(2)当t<10时,求点P的坐标(结果用含t的代数式表示);
(3)以点P为圆心,以OP为半径画圆,当⊙P与菱形OABC的一边所在直线相切时,请直接写出t的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某超市销售一种饮料,每瓶进价为10元.经市场调查表明,当售价在12元到14元之间(含12元,14元)浮动时,日均销售y(瓶)与售价x(元)之间的关系可近似的看作一次函数,且当x=10时,y=500;x=12,y=400.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)应将售价定为每瓶多少元时,所得日均毛利润最大?最大日均毛利润为多少元?(每瓶毛利润=每瓶售价﹣每瓶进价)
查看答案和解析>>
科目: 来源: 题型:
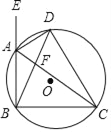
【题目】已知:如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D,AC与BD相交于点F.
(1)求证:DB=DC;
(2)若DA=DF,求证:△BCF∽△BDC.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,O为Rt△ABC的直角边AC上一点,以OC为半径的圆与斜边AB相切于点D,P是弧CD上任意一点,过点P作⊙O的切线,交BC于点M,交AB于点N,已知AB=5,AC=4.
(1)△BMN的周长等于多少;
(2)⊙O的半径.

查看答案和解析>>
科目: 来源: 题型:
【题目】在一个箱子里放有1个白球和2个红球,它们除颜色外其余都相同.
(1)从箱子里摸出1个球,是黑球,这属于什么事件;(填“必然”、“不可能”或“随机”)
(2)从箱子里摸出1个球,放回,摇匀后再摸出一个球,请利用树状图或表格计算,这样先后摸得的两个球都是红球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com