
科目: 来源: 题型:
【题目】已知y=y1+y2 , 其中y1与x成反比例,y2与(x﹣2)成正比例.当x=1时,y=﹣1;x=3时,y=3.求:
(1)y与x的函数关系式;
(2)当x=﹣1时,y的值.
查看答案和解析>>
科目: 来源: 题型:
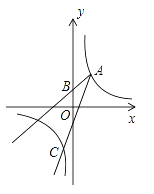
【题目】如图,已知点A(2,3)和点B(0,2),点A在反比例函数y= ![]() 的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为________.
的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
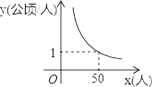
A. 该村人均耕地面积随总人口的增多而增多
B. 该村人均耕地面积y与总人口x成正比例
C. 若该村人均耕地面积为2公顷,则总人口有100人
D. 当该村总人口为50人时,人均耕地面积为1公顷
查看答案和解析>>
科目: 来源: 题型:
【题目】为提升学生的艺术素养,学校计划开设四门艺术选修课:A.书法;B.绘画;C.乐器;D.舞蹈.为了解学生对四门功课的喜欢情况,在全校范围内随机抽取若干名学生进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).将数据进行整理,并绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
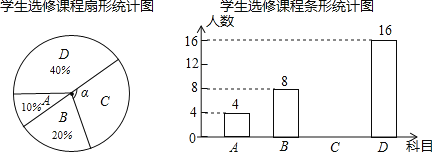
(1)本次调查的学生共有多少人?扇形统计图中∠α的度数是多少?
(2)请把条形统计图补充完整;
(3)学校为举办2018年度校园文化艺术节,决定从A.书法;B.绘画;C.乐器;D.舞蹈四项艺术形式中选择其中两项组成一个新的节目形式,请用列表法或树状图求出选中书法与乐器组合在一起的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】五·一”假期,某公司组织部分员工到A、B、C三地旅游,公司购买前往各地的车票种类、数量绘制成条形统计图,如图,
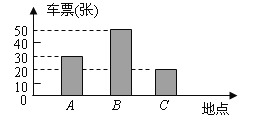
根据统计图回答下列问题:
(1)前往 A地的车票有_______ _张,前往C地的车票占全部车票的________%;
(2)若公司决定采用随机抽取的方式把车票分配给 100 名员工,在看不到车票的条下,每人抽取一张(所有车票的形状、大小、质地完全相同且充分洗匀),那么员工小王抽到去 B 地车票的概率为___ ____;
(3)若最后剩下一张车票时,员工小张、小李都想要,决定采用抛掷一枚各面分别标数字1,2,3,4的正四面体骰子的方法来确定,具体规则是:“每人各抛掷一次,若小张掷得着地一面的数字比小李掷得着地一面的数字大,车票给小张,否则给小李.”试用“列表法或画树状图”的方法分析,这个规则对双方是否公平?
查看答案和解析>>
科目: 来源: 题型:
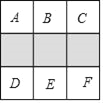
【题目】如图,在正方形方格中,阴影部分是涂黑3个小正方形所形成的图案.
(1)如果将一粒米随机地抛在这个正方形方格上,那么米粒落在阴影部分的概率是多少?
(2)现将方格内空白的小正方形(A,B,C,D,E,F)中任取2个涂黑,得到新图案.请用列表或画树状图的方法求新图案是轴对称图形的概率.
查看答案和解析>>
科目: 来源: 题型:
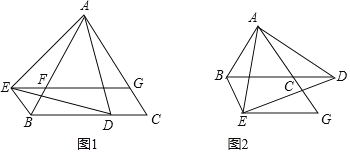
【题目】△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B,C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,交射线AC于点G,连接BE.
(1)如图1所示,当点D在线段BC上时,求证:四边形BCGE是平行四边形;
(2)如图2所示,当点D在BC的延长线上时,(1)中的结论是否成立?并请说明理由;
(3)当点D运动到什么位置时,四边形BCGE是菱形?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
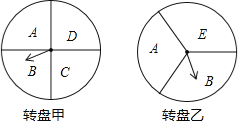
【题目】某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,方式一:转动转盘甲,指针指向A区域时,所购买物品享受9折优惠、指针指向其它区域无优惠;方式二:同时转动转盘甲和转盘乙,若两个转盘的指针指向每个区域的字母相同,所购买物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区城的可能性相同(若指针指向分界线,则重新转动转盘)
(1)若顾客选择方式一,则享受9折优惠的概率为多少;
(2)若顾客选择方式二,请用树状图或列表法列出所有可能,并求顾客享受8折优惠的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点A(3,﹣6)是二次函数y=ax2上的一点,则这二次函数的解析式是 .
【答案】y=﹣![]() x2
x2
【解析】
试题分析:将点A(3,﹣6)代入y=ax2,利用待定系数法法求该二次函数的解析式即可得﹣6=9a,
解得a=﹣![]() ;因此该二次函数的解析式为:y=﹣
;因此该二次函数的解析式为:y=﹣![]() x2.
x2.
考点:待定系数法求二次函数解析式
【题型】填空题
【结束】
15
【题目】在一个不透明的口袋中装有8个红球和若干个白球,它们除颜色外其它完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在40%附近,则口袋中白球可能有________个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com