
科目: 来源: 题型:
【题目】如图,一次函数![]() (
(![]() )的图象与反比例函数
)的图象与反比例函数![]() (
(![]() )的图象相交于点
)的图象相交于点![]() ,
,![]() .
.

(1)求反比例函数和一次函数的解析式;
(2)若直线![]() (
(![]() )与
)与![]() 轴交于点
轴交于点![]() ,
,![]() 轴上是否存在一点
轴上是否存在一点![]() ,使
,使![]() ,若存在,请求出点
,若存在,请求出点![]() 坐标;若不存在,说明理由.
坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年某省实施人才引进政策,对引进人才给予资金扶持和落户优惠,海内外英才纷纷向组织部门递交报名表.为了了解报名人员年龄结构情况,抽样调查了50名报名人员的年龄(单位:岁),将抽样得到的数据分成5组,统计如下表:
分组 | 频数(人数) | 频率 |
30岁以下 | 0.16 | |
大于30岁不大于40岁 | 20 | 0.40 |
大于40岁不大于50岁 | 14 | |
大于50岁不大于60岁 | 6 | 0.12 |
60岁以上 |
(1)请将表格中空格填写完整;
(2)样本数据的中位数落在_____,若把样本数据制成扇形统计图,则“大于30岁不大于40岁”的圆心角为______度;
(3)如果共有2000人报名,请你根据上面数据,估计年龄不大于40岁的报名人员会有多少人?
查看答案和解析>>
科目: 来源: 题型:
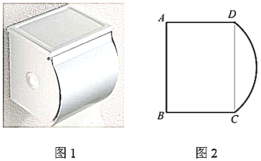
【题目】如图1是一种纸巾盒,由盒身和圆弧盖组成,通过圆弧盖的旋转来开关纸巾盒.如图2是其侧面简化示意图,已知矩形![]() 的长
的长![]() ,宽
,宽![]() ,圆弧盖板侧面
,圆弧盖板侧面![]() 所在圆的圆心
所在圆的圆心![]() 是矩形
是矩形![]() 的中心,绕点
的中心,绕点![]() 旋转开关(所有结果保留小数点后一位).
旋转开关(所有结果保留小数点后一位).
(1)求![]() 所在
所在![]() 的半径长及
的半径长及![]() 所对的圆心角度数;
所对的圆心角度数;
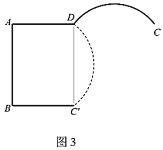
(2)如图3,当圆弧盖板侧面![]() 从起始位置
从起始位置![]() 绕点
绕点![]() 旋转
旋转![]() 时,求
时,求![]() 在这个旋转过程中扫过的的面积.
在这个旋转过程中扫过的的面积.
参考数据:![]() ,
,![]() ,
,![]() 取3.14.
取3.14.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校团委准备暑期组织一次“研学之旅”活动,现有四个“研学”地方可选择:井冈山、龙虎山、庐山、瑞金(其中井冈山、瑞金是红色旅游胜地).校团委决定通过抽签方式确定其中两个地方.
抽签规则:将四个地方分别写在4张完全相同的纸牌正面,把4张纸牌背面朝上,洗匀后放在桌面上,团委书记小明先从中随机抽取一张纸牌,记下地名,再从剩下的纸牌中随机抽取第二张,记下地名.
(1)下列说法中,正确的序号是______.
①第一次“抽中井冈山”的概率是![]() ;
;
②“抽中的是两个地方是红色旅游胜地”是必然事件;
③“抽中的是两个地方是红色旅游胜地”是随机事件;
④“抽中的是两个地方是红色旅游胜地”是不可能事件.
(2)用树状图(或列表法)表示两次抽牌所有可能出现的结果,并求“抽中的是两个地方是红色旅游胜地”的概率.
查看答案和解析>>
科目: 来源: 题型:
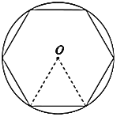
【题目】中国魏晋时期的数学家刘徽首创“割圆术”,奠定了中国圆周率计算在世界上的领先地位.刘徽提出:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”,由此求得圆周率![]() 的近似值.如图,设半径为
的近似值.如图,设半径为![]() 的圆内接正
的圆内接正![]() 边形的周长为
边形的周长为![]() ,圆的直径为
,圆的直径为![]() ,当
,当![]() 时,
时,![]() ,则当
,则当![]() 时,
时,![]() ______.(结果精确到0.01,参考数据:
______.(结果精确到0.01,参考数据:![]() ,
,![]()
![]() )
)
查看答案和解析>>
科目: 来源: 题型:
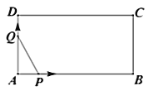
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 从
从![]() 点出发以
点出发以![]() /秒向终点
/秒向终点![]() 运动,动点
运动,动点![]() 同时从
同时从![]() 点出发以
点出发以![]() /秒按
/秒按![]()
![]() 的方向在边
的方向在边![]() ,
,![]() ,
,![]() 上运动,设运动时间为
上运动,设运动时间为![]() (秒),那么
(秒),那么![]() 的面积
的面积![]() 随着时间
随着时间![]() (秒)变化的函数图象大致为( )
(秒)变化的函数图象大致为( )
A.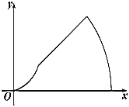 B.
B.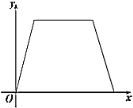 C.
C. D.
D.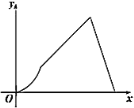
查看答案和解析>>
科目: 来源: 题型:
【题目】在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了下面的折线图,那么符合这一结果的实验最有可能的是( )
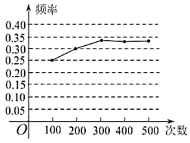
A.洗匀后的1张红桃,2张黑桃牌,从中随机抽取一张牌是黑桃
B.“石头、剪刀、布”的游戏,小王随机出的是“剪刀”
C.掷一枚质地均匀的硬币,落地时结果是“正面向上”
D.掷一个质地均匀的正六面体骰子,落地时朝上面的点数是6
查看答案和解析>>
科目: 来源: 题型:
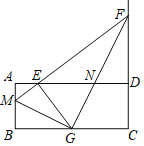
【题目】在矩形ABCD中,AB=4,AD=10,E是AD的一点,且AE=2,M是AB上一点,射线ME交CD的延长线于点F,EG⊥ME交BC于点G,连接MG,FG,FG交AD于点N.
(1)当点M为AB中点时,则DF= ,FG= .(直接写出答案)
(2)在整个运动过程中,![]() 的值是否会变化,若不变,求出它的值;若变化,请说明理由.
的值是否会变化,若不变,求出它的值;若变化,请说明理由.
(3)若△EGN为等腰三角形时,请求出所有满足条件的AM的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com