
科目: 来源: 题型:
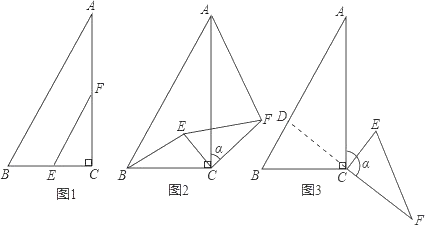
【题目】如图1,在△ABC中,∠ACB=90°,BC=2,∠A=30°,点E,F分别是线段BC,AC的中点,连结EF.
(1)线段BE与AF的位置关系是 ,![]() = .
= .
(2)如图2,当△CEF绕点C顺时针旋转a时(0°<a<180°),连结AF,BE,(1)中的结论是否仍然成立.如果成立,请证明;如果不成立,请说明理由.
(3)如图3,当△CEF绕点C顺时针旋转a时(0°<a<180°),延长FC交AB于点D,如果AD=6﹣2![]() ,求旋转角a的度数.
,求旋转角a的度数.
查看答案和解析>>
科目: 来源: 题型:
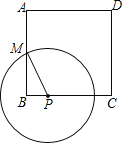
【题目】如图,正方形ABCD的边长为6,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() ,交
,交![]() 轴的负半轴于
轴的负半轴于![]() ,顶点为
,顶点为![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() ;④当
;④当![]() 是等腰直角三角形时,则
是等腰直角三角形时,则![]() ;⑤若
;⑤若![]() ,
,![]() 是一元二次方程
是一元二次方程![]() 的两个根,且
的两个根,且![]() ,则
,则![]() .其中错误的有( )个.
.其中错误的有( )个.
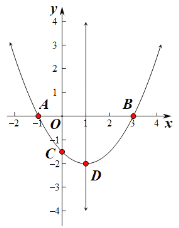
A.5B.4C.3D.2
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形![]() 的边
的边![]() 在
在![]() 轴上,点
轴上,点![]() 坐标为
坐标为![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .若将菱形
.若将菱形![]() 向左平移
向左平移![]() 个单位,使点
个单位,使点![]() 落在该反比例函数图象上,则
落在该反比例函数图象上,则![]() 的值为( ).
的值为( ).
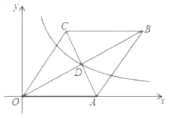
A.1B.2C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线y=﹣![]() x交x轴于点A,点B(6,n)为抛物线上一点.
x交x轴于点A,点B(6,n)为抛物线上一点.
(1)求m与n之间的函数关系;
(2)如图,点C(﹣n,0)在x轴上,且∠BAC=2∠ACB,求m的值;
(3)在(2)的条件下,P为直线BC上方抛物线上一点,过点P作PD∥AB交x轴于点D,DE⊥BC交OP于点E,![]() ,求点P坐标.
,求点P坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】△ABC内接于⊙O,AT切⊙O于点A,AB=BC,且AT∥BC.
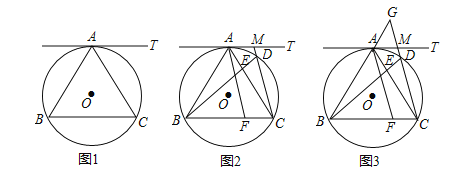
(1)如图1,求证:△ABC是等边三角形;
(2)如图2,点M在射线AT上,连接CM交⊙O于点D,连接BD交AC于点E,AF∥CM交BC于点F,求证:AE=CF;
(3)如图3,在(2)的条件下,延长BA、CM交于点G,若BD=40,CD=25,求AG的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】有一项工程,乙队单独完成所需的时间是甲队单独完成所需时间的2倍,若两队合作4天后,剩下的工作甲单独做还需要6天完成.
(1)求甲、乙两队单独完成这项工程各需多少天;
(2)若甲队每天的报酬是1万元,乙队每天的报酬是0.3万元,要使完成这项工程时的总报酬不超过9.6万元,甲队最多可以工作多少天?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在△OAB中,∠OAB=90°,∠AOB=30°,OB=8.以OB为边,在△OAB
外作等边△OBC,D是OB的中点,连接AD并延长交OC于E.

(1)求证:四边形ABCE是平行四边形;
(2)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】远承中学为了了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机抽取了本校部分学生进行问卷调查(必选且只选一类节目),将调查结果进行整理后,绘制了如下不完整的条形统计图和扇形统计图,其中喜爱体育节目的学生人数比喜爱戏曲节目的学生人数的3倍还多1人.
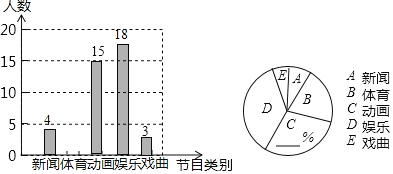
请根据所给信息解答下列问题:
(1)求本次抽取的学生人数;
(2)补全条形图,在扇形统计图中的横线上填上正确的数值;
(3)该校有5000名学生,请你估计该校喜爱娱乐节目的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com