
科目: 来源: 题型:
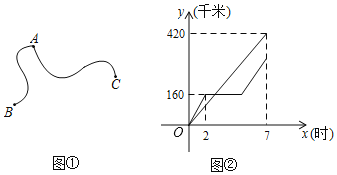
【题目】如图①,甲、乙两车同时从A地出发,分别匀速前往B地与C地,甲车到达B地休息一段时间后原速返回,乙车到达C地后立即返回.两车恰好同时返回A地.图②是两车各自行驶的路程y(千米)与出发时间x(时)之间的函数图象.根据图象解答下列问题:
(1)甲车到达B地休息了 时;
(2)求甲车返回A地途中y与x之间的函数关系式;
(3)当x为何值时,两车与A地的路程恰好相同.(不考虑两车同在A地的情况)
查看答案和解析>>
科目: 来源: 题型:
【题目】某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为176mm~185mm的产品为合格),随机各抽取了20个样品进行检测,过程如下:
收集数据:(单位:mm)
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183
整理数据:
频数 组别 | 165.5~170.5 | 170.5~175.5 | 175.5~180.5 | 180.5~185.5 | 185.5~190.5 | 190.5~195.5 |
甲车间 | 2 | 4 | 5 | 6 | 2 | 1 |
乙车间 | 1 | 2 | a | 6 | 2 | 0 |
分析数据:
车间 | 平均数 | 众数 | 中位数 | 方差 |
甲车间 | 180 | 185 | 180 | 43.1 |
乙车间 | 180 | 180 | 180 | 22.6 |
应用数据:
(1)计算甲车间样品的合格率;
(2)估计乙车间生产的8000个该款新产品中合格产品有多少个?
(3)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
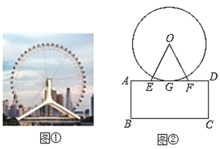
【题目】如图①是长春新地标一一摩天活力城楼顶上的摩天轮,被誉为“长春眼”,如图②是其正面的平面图.已知摩天活力城楼顶AD距地面BC为34米,摩天轮⊙O与楼顶AD近似相切,切点为G.测得∠OEF=∠OFE=67°,EF=27.54米,求摩天轮的最高点到地面BC的距离.(结果精确到0.1米)(参考数据:sin67°=0.92,cos67°0.39,tan67°=2.36)
查看答案和解析>>
科目: 来源: 题型:
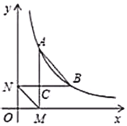
【题目】如图,点![]() 、
、![]() 在函数
在函数![]() (
(![]() ,
,![]() 且
且![]() 是常数)的图像上,且点
是常数)的图像上,且点![]() 在点
在点![]() 的左侧过点
的左侧过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 与
与![]() 的交点为
的交点为![]() ,连结
,连结![]() 、
、![]() .若
.若![]() 和
和![]() 的面积分别为1和4,则
的面积分别为1和4,则![]() 的值为( )
的值为( )
A.4B.![]() C.
C.![]() D.6
D.6
查看答案和解析>>
科目: 来源: 题型:
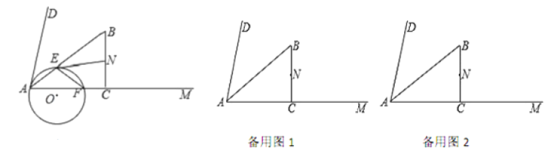
【题目】如图,在![]() 内部做
内部做![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点:动点
的中点:动点![]() 由
由![]() 出发,沿
出发,沿![]() 运动,速度为每秒5个单位,动点
运动,速度为每秒5个单位,动点![]() 由
由![]() 出发,沿
出发,沿![]() 运动,速度为每秒8个单位,当点
运动,速度为每秒8个单位,当点![]() 到达点
到达点![]() 时,两点同时停止运动;过
时,两点同时停止运动;过![]() 、
、![]() 、
、![]() 作
作![]() ;
;
(1)判断![]() 的形状为________,并判断
的形状为________,并判断![]() 与
与![]() 的位置关系为__________;
的位置关系为__________;
(2)求![]() 为何值时,
为何值时,![]() 与
与![]() 相切?求出此时
相切?求出此时![]() 的半径,并比较半径与劣弧
的半径,并比较半径与劣弧![]() 长度的大小;
长度的大小;
(3)直接写出![]() 的内心运动的路径长为__________;(注:当
的内心运动的路径长为__________;(注:当![]() 、
、![]() 、
、![]() 重合时,内心就是
重合时,内心就是![]() 点)
点)
(4)直接写出线段![]() 与
与![]() 有两个公共点时,
有两个公共点时,![]() 的取值范围为__________.
的取值范围为__________.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() ,直线
,直线![]() 与抛物线、
与抛物线、![]() 轴分别相交于
轴分别相交于![]() 、
、![]() .
.

(1)![]() 时,
时,![]() 点的坐标为________;
点的坐标为________;
(2)当![]() 、
、![]() 两点重合时,求
两点重合时,求![]() 的值;
的值;
(3)当![]() 点达到最高时,求抛物线解析式;
点达到最高时,求抛物线解析式;
(4)在抛物线![]() 与
与![]() 轴所围成的封闭图形的边界上,我们把横坐标是整数的点称为“可点”,直接写出
轴所围成的封闭图形的边界上,我们把横坐标是整数的点称为“可点”,直接写出![]() 时“可点”的个数为____.
时“可点”的个数为____.
查看答案和解析>>
科目: 来源: 题型:
【题目】有甲乙两个玩具小汽车在笔直的240米跑道![]() 上进行折返跑游戏,甲从点
上进行折返跑游戏,甲从点![]() 出发,匀速在
出发,匀速在![]() 、
、![]() 之间折返跑,同时乙从点
之间折返跑,同时乙从点![]() 出发,以大于甲的速度匀速在
出发,以大于甲的速度匀速在![]() 、
、![]() 之间折返跑.在折返点的时间忽略不计.
之间折返跑.在折返点的时间忽略不计.

(1)若甲的速度为![]() ,乙的速度为
,乙的速度为![]() ,第一次迎面相遇的时间为
,第一次迎面相遇的时间为![]() ,则
,则![]() 与
与![]() 的关系式___________;
的关系式___________;
(注释:当两车相向而行时相遇是迎面相遇,当两车在![]() 点相遇时也视为迎面相遇)
点相遇时也视为迎面相遇)
(2)如图1,
①若甲乙两车在距![]() 点20米处第一次迎面相遇,则他们在距
点20米处第一次迎面相遇,则他们在距![]() 点_______米第二次迎面相遇:
点_______米第二次迎面相遇:
②若甲乙两车在距![]() 点50米处第一次迎面相遇,则他们在距
点50米处第一次迎面相遇,则他们在距![]() 点__________米第二次迎面相遇;
点__________米第二次迎面相遇;
(3)设甲乙两车在距![]() 点
点![]() 米处第一次迎面相遇,在距
米处第一次迎面相遇,在距![]() 点
点![]() 米处第二次迎面相遇.某同学发现了
米处第二次迎面相遇.某同学发现了![]() 与
与![]() 的函数关系,并画出了部分函数图象(线段
的函数关系,并画出了部分函数图象(线段![]() ,不包括点
,不包括点![]() ,如图2所示).
,如图2所示).
①则![]() _______,并在图2中补全
_______,并在图2中补全![]() 与
与![]() 的函数图象(在图中注明关键点的数据);
的函数图象(在图中注明关键点的数据);
②分别求出各部分图象对应的函数表达式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 是
是![]() 边上的中线,点
边上的中线,点![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,
,![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
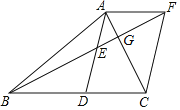
(1)求证:![]() ;
;
(2)若![]() ,①试判断四边形
,①试判断四边形![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
②若![]() ,
,![]() ,直接写出线段
,直接写出线段![]() 的长_________.
的长_________.
查看答案和解析>>
科目: 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为每次连续接球10个,每垫球到位1个记1分.
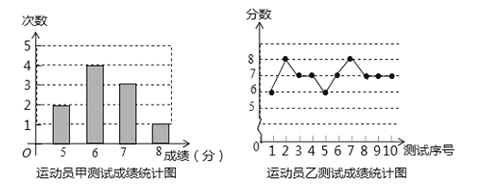
运动员丙测试成绩统计表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 |
| 7 | 5 | 8 |
| 8 | 7 |
运动员丙测试成绩的平均数和众数都是7,
(1)成绩表中的![]() __________,
__________,![]() _________;
_________;
(2)若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?请用你所学过的统计量加以分析说明(参考数据:三人成绩的方差分别为![]() 、
、![]() 、
、![]() )
)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球从乙手中传出,球传一次甲得到球的概率是____.
查看答案和解析>>
科目: 来源: 题型:
【题目】解密数学魔术:魔术师请观众心想一个数,然后将这个数按以下步骤操作:
![]()
魔术师能立刻说出观众想的那个数.
(1)如果小玲想的数是![]() ,请你通过计算帮助她告诉魔术师的结果;
,请你通过计算帮助她告诉魔术师的结果;
(2)如果小明想了一个数计算后,告诉魔术师结果为85,那么魔术师立刻说出小明想的那个数是:__________;
(3)观众又进行了几次尝试,魔术师都能立刻说出他们想的那个数.若设观众心想的数为![]() ,请你按照魔术师要求的运算过程列代数式并化简,再用一句话说出这个魔术的奥妙.
,请你按照魔术师要求的运算过程列代数式并化简,再用一句话说出这个魔术的奥妙.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com