
科目: 来源: 题型:
【题目】某测量队在山脚A处测得山上树顶仰角为45°(如图),测量队在山坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,则山高为( )(精确到1米, ![]() =1.732).
=1.732).
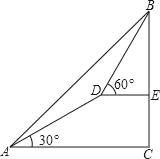
A. 585米 B. 1014米 C. 805米 D. 820米
查看答案和解析>>
科目: 来源: 题型:
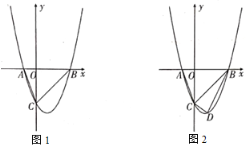
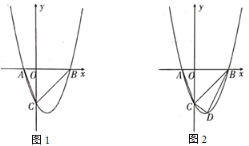
【题目】如图1,在平面直角坐标系中,二次函数![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,(点
两点,(点![]() 在点
在点![]() 的左侧)与
的左侧)与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
(1)求点![]() 、点
、点![]() 和点
和点![]() 的坐标;
的坐标;
(2)如图2,若点![]() 为第四象限内抛物线上一动点,点
为第四象限内抛物线上一动点,点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() .求
.求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值;
的最大值;
(3)抛物线的对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,请直接写出所有点
为等腰三角形?若存在,请直接写出所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】综合与实践:
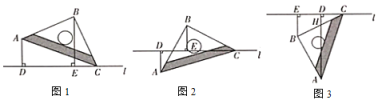
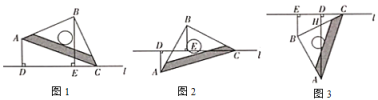
如图1,将一个等腰直角三角尺![]() 的顶点
的顶点![]() 放置在直线
放置在直线![]() 上,
上,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
观察发现:
(1)如图1.当![]() ,
,![]() 两点均在直线
两点均在直线![]() 的上方时,
的上方时,
①猜测线段![]() ,
,![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
②直接写出线段![]() ,
,![]() 与
与![]() 的数量关系;
的数量关系;
操作证明:
(2)将等腰直角三角尺![]() 绕着点
绕着点![]() 逆时针旋转至图2位置时,线段
逆时针旋转至图2位置时,线段![]() ,
,![]() 与
与![]() 又有怎样的数量关系,请写出你的猜想,并写出证明过程;
又有怎样的数量关系,请写出你的猜想,并写出证明过程;
拓广探索:
(3)将等腰直角三用尺![]() 绕着点
绕着点![]() 继续旋转至图3位置时,
继续旋转至图3位置时,![]() 与
与![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() ,请直接写出
,请直接写出![]() 的长度.
的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料,并完成相应任务.
 古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
条线段分成不相等的两部分.使较短线段与较长线段的比等于较长线段与原线段的比,这个相等的比就是![]() ,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
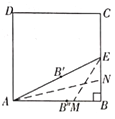
第一步:裁一张正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,然后展平,再折出线段
,然后展平,再折出线段![]() ,再展平;
,再展平;
第二步:将纸片沿![]() 折叠,使
折叠,使![]() 落到线段
落到线段![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平;
,展平;
第三步:沿![]() 折叠,使
折叠,使![]() 落在
落在![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平,这时
,展平,这时![]() 就是
就是![]() 的黄金分割点.
的黄金分割点.
 古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
条线段分成不相等的两部分.使较短线段与较长线段的比等于较长线段与原线段的比,这个相等的比就是![]() ,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
第一步:裁一张正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,然后展平,再折出线段
,然后展平,再折出线段![]() ,再展平;
,再展平;
第二步:将纸片沿![]() 折叠,使
折叠,使![]() 落到线段
落到线段![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平;
,展平;
第三步:沿![]() 折叠,使
折叠,使![]() 落在
落在![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平,这时
,展平,这时![]() 就是
就是![]() 的黄金分割点.
的黄金分割点.

任务:(1)试根据以上操作步骤证明![]() 就是
就是![]() 的黄金分割点;
的黄金分割点;
(2)请写出一个生活中应用黄金分割的实际例子.
查看答案和解析>>
科目: 来源: 题型:
【题目】一声汽笛长鸣,火车开进了蔡家崖.这是我省吕梁革命老区人民期盼已久的客运列车.蔡家崖列车的开通.带动老区驶入了发展红色旅游的快车进.某旅行社对去年“国庆”期间到吕梁观光的游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,回答下列问题:

(1)求本次抽样调查的总人数:
(2)补全条形统计图;
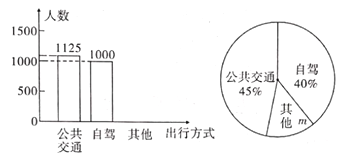
(3)扇形统计图中“其他”部分扇形的圆心角度数为____;
(4)去年“国庆”期问到吕梁观光的旅游者为275万人,则选择自驾方式出行的有多少万人.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年8月.山西龙城将迎来全国第二届青年运动会,盛会将至,整个城市已经进入了全力准备的状态.太职学院足球场作为一个重要比赛场馆.占地面积约24300平方米.总建筑面积4790平方米,设有2476个座位,整体建筑简洁大方,独具特色.2018年3月15日该场馆如期开工,某施工队负责安装该场馆所有座位,在安装完476个座位后,采用新技术,效率比原来提升了![]() .结来比原计划提前4天完成安装任务.求原计划每天安装多少个座位.
.结来比原计划提前4天完成安装任务.求原计划每天安装多少个座位.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在平面直角坐标系中,二次函数![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,(点
两点,(点![]() 在点
在点![]() 的左侧)与
的左侧)与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
(1)求点![]() 、点
、点![]() 和点
和点![]() 的坐标;
的坐标;
(2)如图2,若点![]() 为第四象限内抛物线上一动点,点
为第四象限内抛物线上一动点,点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() .求
.求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值;
的最大值;
(3)抛物线的对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,请直接写出所有点
为等腰三角形?若存在,请直接写出所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】综合与实践:
如图1,将一个等腰直角三角尺![]() 的顶点
的顶点![]() 放置在直线
放置在直线![]() 上,
上,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
观察发现:
(1)如图1.当![]() ,
,![]() 两点均在直线
两点均在直线![]() 的上方时,
的上方时,
①猜测线段![]() ,
,![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
②直接写出线段![]() ,
,![]() 与
与![]() 的数量关系;
的数量关系;
操作证明:
(2)将等腰直角三角尺![]() 绕着点
绕着点![]() 逆时针旋转至图2位置时,线段
逆时针旋转至图2位置时,线段![]() ,
,![]() 与
与![]() 又有怎样的数量关系,请写出你的猜想,并写出证明过程;
又有怎样的数量关系,请写出你的猜想,并写出证明过程;
拓广探索:
(3)将等腰直角三用尺![]() 绕着点
绕着点![]() 继续旋转至图3位置时,
继续旋转至图3位置时,![]() 与
与![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() ,请直接写出
,请直接写出![]() 的长度.
的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料,并完成相应任务.
 古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
条线段分成不相等的两部分.使较短线段与较长线段的比等于较长线段与原线段的比,这个相等的比就是![]() ,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
第一步:裁一张正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,然后展平,再折出线段
,然后展平,再折出线段![]() ,再展平;
,再展平;
第二步:将纸片沿![]() 折叠,使
折叠,使![]() 落到线段
落到线段![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平;
,展平;
第三步:沿![]() 折叠,使
折叠,使![]() 落在
落在![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平,这时
,展平,这时![]() 就是
就是![]() 的黄金分割点.
的黄金分割点.

 古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
古希腊数学家,天文学家欧多克索斯(Eudoxus,约前400—前347)曾提出:能否将一
条线段分成不相等的两部分.使较短线段与较长线段的比等于较长线段与原线段的比,这个相等的比就是![]() ,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
,黄金分割在我们生活中有广泛运用.黄金分割点也可以用折纸的方式得到.
第一步:裁一张正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,然后展平,再折出线段
,然后展平,再折出线段![]() ,再展平;
,再展平;
第二步:将纸片沿![]() 落到线段
落到线段![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平;
,展平;
第三步:沿![]() 折叠,使
折叠,使![]() 落在
落在![]() 上,
上,![]() 的对应点为
的对应点为![]() ,展平,这时
,展平,这时![]() 就是
就是![]() 的黄金分割点.
的黄金分割点.

任务:(1)试根据以上操作步骤证明![]() 就是
就是![]() 的黄金分割点;
的黄金分割点;
(2)请写出一个生活中应用黄金分割的实际例子.
查看答案和解析>>
科目: 来源: 题型:
【题目】一声汽笛长鸣,火车开进了蔡家崖.这是我省吕梁革命老区人民期盼已久的客运列车.蔡家崖列车的开通.带动老区驶入了发展红色旅游的快车进.某旅行社对去年“国庆”期间到吕梁观光的游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,回答下列问题:

(1)求本次抽样调查的总人数:
(2)补全条形统计图;
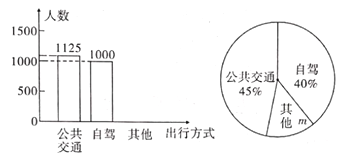
(3)扇形统计图中“其他”部分扇形的圆心角度数为____;
(4)去年“国庆”期问到吕梁观光的旅游者为275万人,则选择自驾方式出行的有多少万人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com