
科目: 来源: 题型:
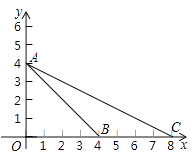
【题目】如图,在平面直角坐标系xOy中,点A,B,C的坐标分别是(0,4),(4,0),(8,0),⊙M是△ABC的外接圆,则点M的坐标为___________.
查看答案和解析>>
科目: 来源: 题型:
【题目】一张三角形纸片ABC,其中∠C=90,AC=6,BC=8.小静同学将纸片做两次折叠:第一次使点A落在C处,折痕记为m;然后将纸片展平做第二次折叠,使点A落在B处,折痕记为n.则m,n的大小关系是_________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点A,B,C,D在⊙O上,弦AD的延长线与弦BC的延长线相交于点E.用①AB是⊙O的直径,②CB=CE,③AB=AE中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为( )
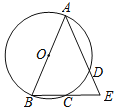
A.0B.1C.2D.3
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面内,对于给定的![]() ,如果存在一个半圆或优弧与
,如果存在一个半圆或优弧与![]() 的两边相切,且该弧上的所有点都在
的两边相切,且该弧上的所有点都在![]() 的内部或边上,则称这样的弧为
的内部或边上,则称这样的弧为![]() 的内切弧.当内切弧的半径最大时,称该内切弧为
的内切弧.当内切弧的半径最大时,称该内切弧为![]() 的完美内切弧.(注:弧的半径指该弧所在圆的半径)
的完美内切弧.(注:弧的半径指该弧所在圆的半径)
在平面直角坐标系![]() 中,
中,![]() .
.
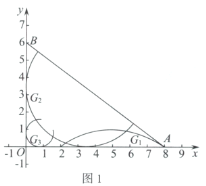
(1)如图1,在弧![]() ,弧
,弧![]() ,弧
,弧![]() 中,是
中,是![]() 的内切弧的是____________;
的内切弧的是____________;
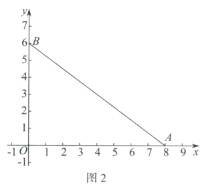
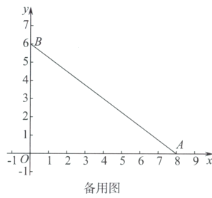
(2)如图2,若弧G为![]() 的内切弧,且弧G与边
的内切弧,且弧G与边![]() 相切,求弧G的半径的最大值;
相切,求弧G的半径的最大值;
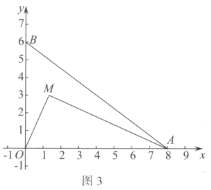
(3)如图3,动点![]() ,连接
,连接![]() .
.
①直接写出![]() 的完美内切弧的半径的最大值;
的完美内切弧的半径的最大值;
②记①中得到的半径最大时的完美内切弧为弧T.点P为弧T上的一个动点,过点P作x轴的垂线,分别交x轴和直线![]() 于点D,E,点F为线段
于点D,E,点F为线段![]() 的中点,直接写出线段
的中点,直接写出线段![]() 长度的取值范围.
长度的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,等边三角形![]() 中,D为
中,D为![]() 边上一点,满足
边上一点,满足![]() ,连接
,连接![]() ,以点A为中心,将射线
,以点A为中心,将射线![]() 顺时针旋转60°,与
顺时针旋转60°,与![]() 的外角平分线
的外角平分线![]() 交于点E.
交于点E.
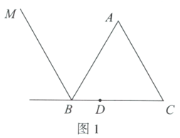
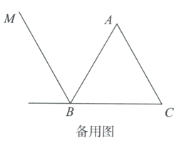
(1)依题意补全图1;
(2)求证:![]() ;
;
(3)若点B关于直线![]() 的对称点为F,连接
的对称点为F,连接![]() .
.
①求证:![]() ;
;
②若![]() 成立,直接写出
成立,直接写出![]() 的度数为_________°.
的度数为_________°.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知二次函数
中,已知二次函数![]() 的图象与x轴交于点
的图象与x轴交于点![]() ,与y轴交于点B,将其图象在点A,B之间的部分(含A,B两点)记为F.
,与y轴交于点B,将其图象在点A,B之间的部分(含A,B两点)记为F.
(1)求点B的坐标及该函数的表达式;
(2)若二次函数![]() 的图象与F只有一个公共点,结合函数图象,求a的取值范围.
的图象与F只有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在四边形![]() 中,对角线
中,对角线![]() 平分
平分![]() .为了研究图中线段之间的数量关系,设
.为了研究图中线段之间的数量关系,设![]() .
.
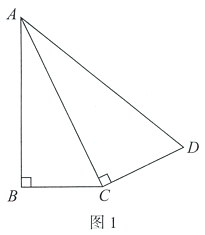
(1)由题意可得![]() ,(在括号内填入图1中相应的线段)y关于x的函数表达式为
,(在括号内填入图1中相应的线段)y关于x的函数表达式为![]() ________;
________;
(2)如图2,在平面直角坐标系![]() 中,根据(1)中y关于x的函数表达式描出了其图象上的一部分点,请依据描出的点画出该函数的图象;
中,根据(1)中y关于x的函数表达式描出了其图象上的一部分点,请依据描出的点画出该函数的图象;
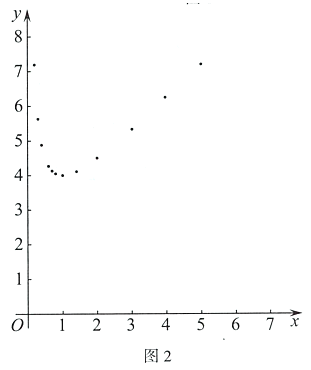
(3)结合函数图象,解决问题:
①写出该函数的一条性质:__________________________;
②估计![]() 的最小值为__________.(结果精确到0.1)
的最小值为__________.(结果精确到0.1)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]() .M是函数
.M是函数![]() 图象上一点,过M作x轴的平行线交直线
图象上一点,过M作x轴的平行线交直线![]() 于点N.
于点N.
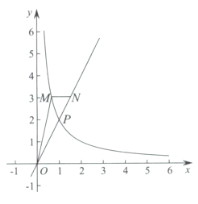
(1)求k和p的值;
(2)设点M的横坐标为m.
①求点N的坐标;(用含m的代数式表示)
②若![]() 的面积大于
的面积大于![]() ,结合图象直接写出m的取值范围.
,结合图象直接写出m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】坚持节约资源和保护环境是我国的基本国策,国家要求加强生活垃圾分类回收与再生资源回收有效衔接,提高全社会资源产出率,构建全社会的资源循环利用体系.
图1反映了2014—2019年我国生活垃圾清运量的情况.

图2反映了2019年我国G市生活垃圾分类的情况.
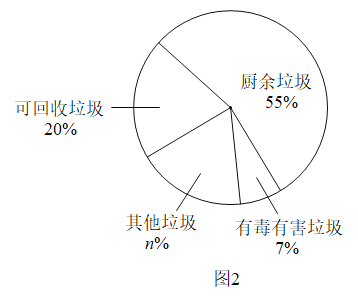
根据以上材料回答下列问题:
(1)图2中,n的值为___________;
(2)2014—2019年,我国生活垃圾清运量的中位数是_________;
(3)据统计,2019年G市清运的生活垃圾中可回收垃圾约为0.02亿吨,所创造的经济总价值约为40亿元.若2019年我国生活垃圾清运量中,可回收垃圾的占比与G市的占比相同,根据G市的数据估计2019年我国可回收垃圾所创造的经济总价值是多少.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是小王同学“过直线外一点作该直线的平行线”的尺规作图过程.
已知:直线l及直线l外一点P.
求作:直线![]() ,使得
,使得![]() .
.

作法:如图,
①在直线l外取一点A,作射线![]() 与直线l交于点B,
与直线l交于点B,
②以A为圆心,![]() 为半径画弧与直线l交于点C,连接
为半径画弧与直线l交于点C,连接![]() ,
,
③以A为圆心,![]() 为半径画弧与线段
为半径画弧与线段![]() 交于点
交于点![]() ,
,
则直线![]() 即为所求.
即为所求.
根据小王设计的尺规作图过程,,
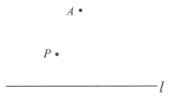
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵![]() ,
,
∴![]() ,(______________________)(填推理的依据).
,(______________________)(填推理的依据).
∵![]() __________,
__________,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() (____________________)(填推理的依据).
(____________________)(填推理的依据).
即![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com