
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]() .M是函数
.M是函数![]() 图象上一点,过M作x轴的平行线交直线
图象上一点,过M作x轴的平行线交直线![]() 于点N.
于点N.
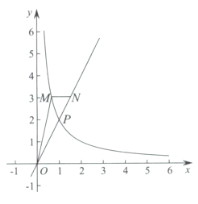
(1)求k和p的值;
(2)设点M的横坐标为m.
①求点N的坐标;(用含m的代数式表示)
②若![]() 的面积大于
的面积大于![]() ,结合图象直接写出m的取值范围.
,结合图象直接写出m的取值范围.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ;②
;②![]() 或者
或者![]() .
.
【解析】
(1)将点![]() 代入反比例函数的解析式可求出
代入反比例函数的解析式可求出![]() 的值,从而可得点P坐标,再将其代入直线
的值,从而可得点P坐标,再将其代入直线![]() 即可得出k的值;
即可得出k的值;
(2)①先根据反比例函数的解析式求出点M的纵坐标,从而可得点N的纵坐标,再将其代入直线的解析式可得点N的横坐标,从而可得出答案;
②分![]() 和
和![]() 两种情况,分别求出MN的长和MN边上的高,再根据三角形的面积公式列出不等式,求解即可得.
两种情况,分别求出MN的长和MN边上的高,再根据三角形的面积公式列出不等式,求解即可得.
(1)依题意,点![]() 在函数
在函数![]() 的图象上
的图象上
可得![]() ,则点
,则点![]()
将![]() 代入直线
代入直线![]() ,得
,得![]()
综上,![]() ,
,![]() ;
;
(2)①由于M是函数![]() 图象上一点,且点M的横坐标为m
图象上一点,且点M的横坐标为m
可得点M的纵坐标为![]()
则点![]()
又因为过M作x轴的平行线交直线![]() 于点N
于点N
则点N的纵坐标为![]()
当![]() 时,
时,![]() ,解得
,解得![]()
则点N的坐标为![]() ;
;
②由题意得:![]() 且
且![]() (因为当
(因为当![]() 时,点M、N重合,不能构成
时,点M、N重合,不能构成![]() )
)
因此,分以下两种情况:
(ⅰ)当![]() 时,
时,![]() ,边MN上的高为
,边MN上的高为![]()
则![]()
解得![]()
结合![]() 得:
得:![]()
(ⅱ)当![]() 时,
时,![]() ,边MN上的高为
,边MN上的高为![]()
则![]()
解得![]() (符合题设)或
(符合题设)或![]() (不符题设,舍去)
(不符题设,舍去)
综上,m的取值范围为![]() 或者
或者![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,双曲线y1=![]() 与直线y2=
与直线y2=![]() 的图象交于A、B两点.已知点A的坐标为(4,1),点P(a,b)是双曲线y1=
的图象交于A、B两点.已知点A的坐标为(4,1),点P(a,b)是双曲线y1=![]() 上的任意一点,且0<a<4.
上的任意一点,且0<a<4.
(1)分别求出y1、y2的函数表达式;
(2)连接PA、PB,得到△PAB,若4a=b,求三角形ABP的面积;
(3)当点P在双曲线y1=![]() 上运动时,设PB交x轴于点E,延长PA交x轴于点F,判断PE与PF的大小关系,并说明理由.
上运动时,设PB交x轴于点E,延长PA交x轴于点F,判断PE与PF的大小关系,并说明理由.
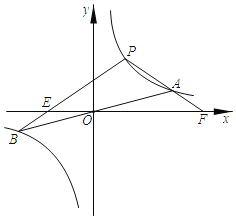
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BC⊥x轴,垂足为D,边AB所在直线分别交x轴、y轴于点E、F,且AF=EF,反比例函数y=![]() 的图象经过A、C两点,已知点A(2,n).
的图象经过A、C两点,已知点A(2,n).
(1)求AB所在直线对应的函数表达式;(2)求点C的坐标.
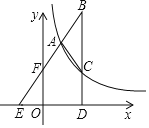
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是某企业甲、乙两位员工的能力测试结果的网状图,以O为圆心的五个同心圆分别代表能力水平的五个等级由低到高分别赋分1至5分,由原点出发的五条线段分别指向能力水平的五个维度,网状图能够更加直观的描述测试者的优势和不足,观察图形,有以下几个推断:
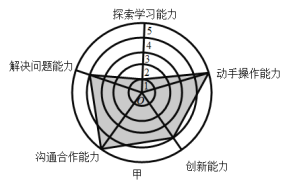
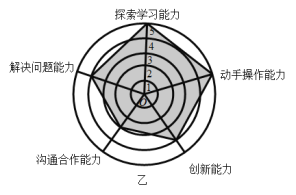
①甲和乙的动手操作能力都很强;
②缺少探索学习的能力是甲自身的不足;
③与甲相比乙需要加强与他人的沟通合作能力;
④乙的综合评分比甲要高.
其中合理的是( )
A.①③B.②④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
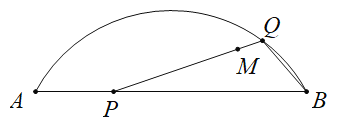
【题目】如图,M是弦![]() 与弧
与弧![]() 所围成的图形的内部的一个定点,P是弦
所围成的图形的内部的一个定点,P是弦![]() 上一动点,连接
上一动点,连接![]() 并延长交弧
并延长交弧![]() 于点Q,连接
于点Q,连接![]() .
.
已知![]() ,设A,P两点间的距离为
,设A,P两点间的距离为![]() ,P,Q两点间距离为
,P,Q两点间距离为![]() ,
,![]() 两点间距离为
两点间距离为![]() .
.
小明根据学习函数的经验,分别对函数![]() 随自变量x的变化而变化的规律进行了研究.下面是小明的探究过程,请补充完整.
随自变量x的变化而变化的规律进行了研究.下面是小明的探究过程,请补充完整.
(1)按照如表中自变量x的值进行取点、画图、测量,分别得到了![]() 与x的几组对应值,补全下表:
与x的几组对应值,补全下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 5.24 | 4.24 | 3.24 | 1.54 | 1.79 | 3.47 | |
| 1.31 | 1.34 | 1.42 | 1.54 | 1.80 | 2.45 | 3.47 |
(2)在同一平面直角坐标系![]() 中,描出表中各组数值对应的点
中,描出表中各组数值对应的点![]() 和
和![]() 并画出函数
并画出函数![]() 的图象;
的图象;
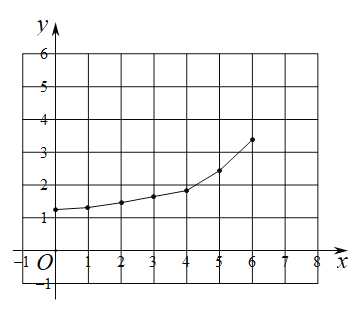
(3)结合函数图象,解决问题:当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长度约_________
的长度约_________![]() .(精确到0.1)
.(精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
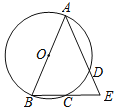
【题目】如图,点A,B,C,D在⊙O上,弦AD的延长线与弦BC的延长线相交于点E.用①AB是⊙O的直径,②CB=CE,③AB=AE中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
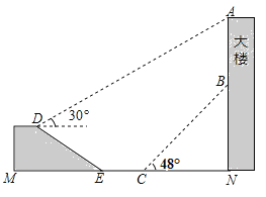
【题目】如图,大楼AN上悬挂一条幅AB,小颖在坡面D处测得条幅顶部A的仰角为30°,沿坡面向下走到坡脚E处,然后向大楼方向继续行走10米来到C处,测得条幅的底部B的仰角为48°,此时小颖距大楼底端N处20米.已知坡面DE=20米,山坡的坡度i=![]() ,且D、M、E、C、N、B、A在同一平面内,M、E、C、N在同一条直线上.
,且D、M、E、C、N、B、A在同一平面内,M、E、C、N在同一条直线上.
(1)求BN的长度;
(2)求条幅AB的长度(结果保留根号).
(参考数据:sin48°≈![]() ,tan48°≈
,tan48°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 铀交于
铀交于![]() 两点(点
两点(点![]() 作点
作点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() 且
且![]() ,点
,点![]() 为抛物线
为抛物线![]() 的对称轴右侧图象上的一点.
的对称轴右侧图象上的一点.
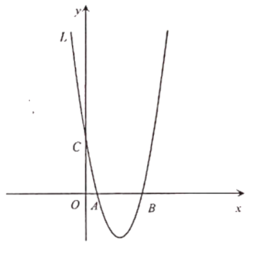
(1)a的值为_ ,抛物线的顶点坐标为_ ;
(2)设抛物线![]() 在点
在点![]() 和点
和点![]() 之间部分(含点
之间部分(含点![]() 和点
和点![]() )的最高点与最低点的纵坐标之差为
)的最高点与最低点的纵坐标之差为![]() ,求
,求![]() 关于
关于![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围;
的取值范围;
(3)当点![]() 的坐标满足:
的坐标满足:![]() 时,连接
时,连接![]() ,若
,若![]() 为线段
为线段![]() 上一点,且
上一点,且![]() 分四边形
分四边形![]() 的面积为相等两部分,求点
的面积为相等两部分,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() :
:![]() 相交于
相交于![]() 和点
和点![]() 两点.
两点.
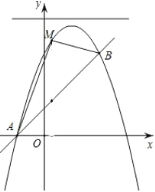
⑴求抛物线![]() 的函数表达式;
的函数表达式;
⑵若点![]() 是位于直线
是位于直线![]() 上方抛物线上的一动点,以
上方抛物线上的一动点,以![]() 为相邻两边作平行四边形
为相邻两边作平行四边形![]() ,当平行四边形
,当平行四边形![]() 的面积最大时,求此时四边形
的面积最大时,求此时四边形![]() 的面积
的面积![]() 及点
及点![]() 的坐标;
的坐标;
⑶在抛物线![]() 的对称轴上是否存在定点
的对称轴上是否存在定点![]() ,使抛物线
,使抛物线![]() 上任意一点
上任意一点![]() 到点
到点![]() 的距离等于到直线
的距离等于到直线![]() 的距离,若存在,求出定点
的距离,若存在,求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com