
科目: 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,A,B,C均为格点.
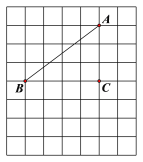
(1)![]() 的面积等于;
的面积等于;
(2)请用无刻度的直尺,在如图所示的网格中画出![]() 的角平分线BD,并在AB边上画出点P,使得
的角平分线BD,并在AB边上画出点P,使得![]() ,并简要说明
,并简要说明![]() 的角平分线BD及点P的位置是如何找到的(不要求证明)
的角平分线BD及点P的位置是如何找到的(不要求证明)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,将纸片展平,再次折叠纸片,使点A落在EF上的点N处,并使折痕经过点B,得到折痕BM,再展平纸片,连接MN,BN.下列结论一定正确的是( )
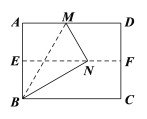
A.![]() B.
B.![]()
C.BM与EN互相平分D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点P和图形M,给出如下定义:Q为图形M上任意一点,如果
中的点P和图形M,给出如下定义:Q为图形M上任意一点,如果![]() 两点间的距离有最大值,那么称这个最大值为点P与图形M间的开距离,记作
两点间的距离有最大值,那么称这个最大值为点P与图形M间的开距离,记作![]() .已知直线
.已知直线![]() 与x轴交于点A,与y轴交于点B,
与x轴交于点A,与y轴交于点B,![]() 的半径为1.
的半径为1.
(1)若![]() ,
,
①求![]() 的值;
的值;
②若点C在直线![]() 上,求
上,求![]() 的最小值;
的最小值;
(2)以点A为中心,将线段![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,点E在线段
,点E在线段![]() 组成的图形上,若对于任意点E,总有
组成的图形上,若对于任意点E,总有![]() ,直接写出b的取值范围.
,直接写出b的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与y轴交于点
与y轴交于点![]() .
.
(1)求c的值;
(2)当![]() 时,求抛物线顶点的坐标;
时,求抛物线顶点的坐标;
(3)已知点![]() ,若抛物线
,若抛物线![]() 与线段
与线段![]() 有两个公共点,结合函数图象,求a的取值范围.
有两个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与x轴交于点A,与y轴交于点B,直线
与x轴交于点A,与y轴交于点B,直线![]() 与x轴交于点C.
与x轴交于点C.

(1)求点B的坐标;
(2)横、纵坐标都是整数的点叫做整点.记线段![]() 围成的区域(不含边界)为G.
围成的区域(不含边界)为G.
①当![]() 时,结合函数图象,求区域G内整点的个数;
时,结合函数图象,求区域G内整点的个数;
②若区域G内恰有2个整点,直接写出k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 是半圆的直径,P是半圆与直径
是半圆的直径,P是半圆与直径![]() 所围成的图形的外部的一定点,D是直径
所围成的图形的外部的一定点,D是直径![]() 上一动点,连接
上一动点,连接![]() 并延长,交半圆于点C,连接
并延长,交半圆于点C,连接![]() .已知
.已知![]() ,设
,设![]() 两点间的距离为
两点间的距离为![]() ,
,![]() 两点之间的距离为
两点之间的距离为![]() 两点之间的距离为
两点之间的距离为![]() .
.
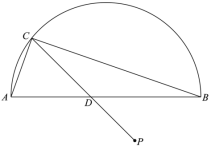
小明根据学习函数的经验,分别对函数![]() 随自变量x的变化而变化的规律进行了探究.
随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)按照下表自变量x的值进行取点、画图、测量,分别得到![]() 与x的几组对应值;
与x的几组对应值;
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0.47 | 1.31 | 5.02 | 5.91 | 6 | |
| 6 | 5.98 | 5.86 | 5.26 | 3.29 | 1.06 | 0 |
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() 的图象;
的图象;
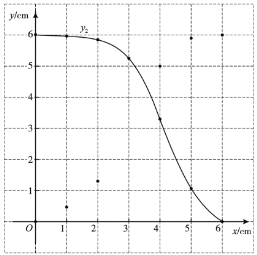
(3)结合函数图象,解决问题:当![]() 有一个角的正弦值为
有一个角的正弦值为![]() 时,
时,![]() 的长约为_____cm.
的长约为_____cm.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解某地区企业信息化发展水平,从该地区中随机抽取50家企业调研,针对体现企业信息化发展水平的A和B两项指标进行评估,获得了它们的成绩(十分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
a.A项指标成绩的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ):
):
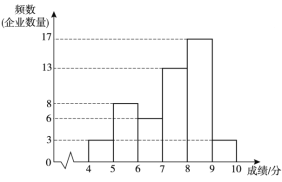
b.A项指标成绩在![]() 这一组的是:
这一组的是:
7.2 7.3 7.5 7.67 7.7 7.71 7.75 7.82 7.86 7.9 7.92 7.93 7.97
c.![]() 两项指标成绩的平均数、中位数、众数如下:
两项指标成绩的平均数、中位数、众数如下:
平均数 | 中位数 | 众数 | |
A项指标成绩 | 7.37 | m | 8.2 |
B项指标成绩 | 7.21 | 7.3 | 8 |
根据以上信息,回答下列问题:
(1)写出表中m的值
(2)在此次调研评估中,某企业A项指标成绩和B项指标成绩都是7.5分,该企业成绩排名更靠前的指标是______________(填“A”或“B”),理由是_____________;
(3)如果该地区有500家企业,估计A项指标成绩超过7.68分的企业数量.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程.
已知:直线l及直线l外一点P.
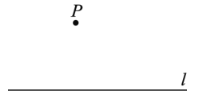
求作:直线![]() ,使得
,使得![]() .
.
作法:如图,
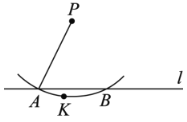
①任意取一点K,使点K和点P在直线l的两旁;
②以P为圆心,![]() 长为半径画弧,交l于点
长为半径画弧,交l于点![]() ,连接
,连接![]() ;
;
③分别以点![]() 为圆心,以
为圆心,以![]() 长为半径画弧,两弧相交于点Q(点Q和点A在直线
长为半径画弧,两弧相交于点Q(点Q和点A在直线![]() 的两旁);
的两旁);
④作直线![]() .
.
所以直线![]() 就是所求作的直线.
就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接![]() ,
,
![]() ______,
______,![]() ______,
______,
![]() 四边形
四边形![]() 是平行四边形(__________)(填推理依据).
是平行四边形(__________)(填推理依据).
![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】正方形![]() 的边长为4,点
的边长为4,点![]() 在对角线
在对角线![]() 上(可与点
上(可与点![]() 重合),
重合),![]() ,点
,点![]() 在正方形的边上.下面四个结论中,
在正方形的边上.下面四个结论中,
①存在无数个四边形![]() 是平行四边形;
是平行四边形;
②存在无数个四边形![]() 是菱形;
是菱形;
③存在无数个四边形![]() 是矩形;
是矩形;
④至少存在一个四边形![]() 是正方形.
是正方形.
所有正确结论的序号是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com