
科目: 来源: 题型:
【题目】某社区为了加强社区居民对新型冠状病非肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《2020年新型冠状病毒防治全国统一考试(全国卷)》试卷,社区管理员随机从甲、乙两个小区各抽取![]() 名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下:
名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下:
收集数据
甲小区:![]()
![]()
乙小区:![]()
![]()
整理数据
成绩 |
|
|
|
|
甲小区 |
|
|
|
|
乙小区 |
|
|
|
|
分析数据
统计量 | 平均数 | 中位教 | 众数 |
甲小区 |
|
|
|
乙小区 |
|
|
|
应用数据
(1)填空:![]() _ _;
_ _;
(2)若甲小区共有![]() 人参与答卷,请估计甲小区成绩大于
人参与答卷,请估计甲小区成绩大于![]() 分的人数;
分的人数;
(3)社区管理员看完统计数据,认为甲小区对新型冠状病毒肺炎防护知识掌握更好,请你写出社区管理员的理由(至少写出一条) .
查看答案和解析>>
科目: 来源: 题型:
【题目】在奉贤创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:
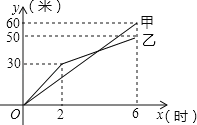
(1)求乙队在2≤x≤6的时段内,y与x之间的函数关系式;
(2)如果甲队施工速度不变,乙队在开挖6小时后,施工速度增加到12米/时,结果两队同时完成了任务.求甲队从开始施工到完工所铺设的彩色道砖的长度为多少米?
查看答案和解析>>
科目: 来源: 题型:
【题目】[问题提出]
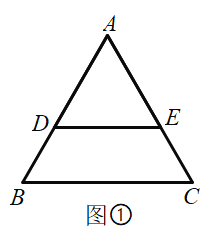
(1)如图![]() 均为等边三角形,点
均为等边三角形,点![]() 分别在边
分别在边![]() 上.将
上.将![]() 绕点
绕点![]() 沿顺时针方向旋转,连结
沿顺时针方向旋转,连结![]() .在图
.在图![]() 中证明
中证明![]() .
.

[学以致用]
(2)在![]() 的条件下,当点
的条件下,当点![]() 在同一条直线上时,
在同一条直线上时,![]() 的大小为 度.
的大小为 度.
[拓展延伸]
(3)在![]() 的条件下,连结
的条件下,连结![]() .若
.若![]() 直接写出
直接写出![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以每秒
方向以每秒![]() 个单位长度的速度向终点
个单位长度的速度向终点![]() 运动(点
运动(点![]() 不与
不与![]() 重合),过点
重合),过点![]() 作
作![]() 交折线
交折线![]() 于点
于点![]() 以
以![]() 为边问下作正方形
为边问下作正方形![]() 点
点![]() 落在边
落在边![]() 上设点
上设点![]() 运动的时间为
运动的时间为![]() (秒).
(秒).

(1)直接用含![]() 的代数式表示线段
的代数式表示线段![]() 的长.
的长.
(2)当点![]() 落在边
落在边![]() 上时,求
上时,求![]() 的值.
的值.
(3)当正方形![]() 与
与![]() 重叠部分图形为四边形时,设四边形的面积为
重叠部分图形为四边形时,设四边形的面积为![]() (平方单位),求
(平方单位),求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)点![]() 为边
为边![]() 的中点,直接写出直线
的中点,直接写出直线![]() 将正方形
将正方形![]() 分成的两部分图形的面积比为
分成的两部分图形的面积比为![]() 时
时![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数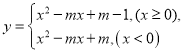 将此函数的图象记为
将此函数的图象记为![]() .
.
(1)当![]() 时,
时,
![]() 直接写出此函数的函数表达式.
直接写出此函数的函数表达式.
![]() 点
点![]() 在图象
在图象![]() 上,求点
上,求点![]() 的坐标.
的坐标.
![]() 点
点![]() 在图象
在图象![]() 上,求
上,求![]() 的值.
的值.
(2)设图象![]() 最低点的纵坐标为
最低点的纵坐标为![]() .当
.当![]() 时,直接写出
时,直接写出![]() 的值.
的值.
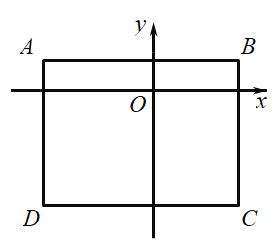
(3)矩形![]() 的顶点坐标分别为
的顶点坐标分别为![]() 若函数
若函数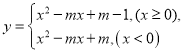 在
在![]() 范围内的图象与矩形
范围内的图象与矩形![]() 的边有且只有一个公共点,直接写出此时
的边有且只有一个公共点,直接写出此时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】小李经营一个社区快递网点,负责周边快件收发,由于疫情原因,到2020年2月12 日网点才可以复工,而该网点的另外两名员工因为办理复工手续,将分别在2月15日和2月26日返岗,工作据大数据显示,预计从复工之日开始,每日到达该网点的快件数量![]() (件)与第
(件)与第![]() 天(2月12日为第
天(2月12日为第![]() 天)满足:
天)满足: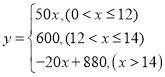 .已知一位快递员日均派送快件量为
.已知一位快递员日均派送快件量为![]() 件,通过加班最高可派送
件,通过加班最高可派送![]() 件.
件.
![]() 前三天小李派送的快件总量为_ 件;
前三天小李派送的快件总量为_ 件;
![]() 以最高派送量派送快件还有剩余时,则当天剩余快件留到第二天优先派送,
以最高派送量派送快件还有剩余时,则当天剩余快件留到第二天优先派送,
①到第十天结束时,滞留的快件共有 件; 到第十四天结束时,滞留的快件共有__件;
②2月18日后快递激增爆仓,小李和员工每天加班派送,根据现有快递数量的变化趋势,从2月19日开始计算,小李至少要加班几天才可以不用加班派送.(即小李不加班派送的情况下,快递点没有滞留件)
![]() 到了3月5日,全国疫情稳定,预计每日到达网点的快件数量将按新趋势变化,“女神节”期间(3月6日-9日)日均快件量为
到了3月5日,全国疫情稳定,预计每日到达网点的快件数量将按新趋势变化,“女神节”期间(3月6日-9日)日均快件量为![]() 件,3月10日起日均快件量稳定在
件,3月10日起日均快件量稳定在![]() 件.此时小李接到快递总公司新规定:从3月10日开始,到达的快件必须当天派送完毕,否则将扣除滞留快件滞留费
件.此时小李接到快递总公司新规定:从3月10日开始,到达的快件必须当天派送完毕,否则将扣除滞留快件滞留费![]() 元/件天(之前滞留的快件从3月10日0时开始收取滞留费)为此,小李想到从市场招聘____名临时工帮助派送快递,若临时工基本工资
元/件天(之前滞留的快件从3月10日0时开始收取滞留费)为此,小李想到从市场招聘____名临时工帮助派送快递,若临时工基本工资![]() 元/天,外加派送费
元/天,外加派送费![]() 元/件临时工一天最多可派送快件
元/件临时工一天最多可派送快件![]() 件,为了将支出降到最低,小李应该聘请临时工几天,派送快件共多少件?此时最低支出多少元钱?直接写出你的答案.
件,为了将支出降到最低,小李应该聘请临时工几天,派送快件共多少件?此时最低支出多少元钱?直接写出你的答案.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,四边形![]() 内接于直径为
内接于直径为![]() 的圆,
的圆,![]() .
.
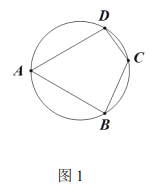
(1)①![]() _ ;
_ ;
②四边形![]() 的周长最大值为_ ;
的周长最大值为_ ;
![]() 如图2,延长
如图2,延长![]() 相交于点
相交于点![]() ,延长
,延长![]() 相交于点
相交于点![]() 求
求![]() 与的
与的![]() 积;
积;
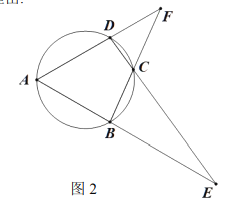
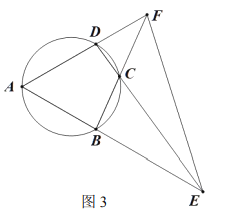
![]() 如图3,连接
如图3,连接![]() 请问在线段
请问在线段![]() 上是否存在点
上是否存在点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,若存在,请证明;若不存在,请说明理由.
对称,若存在,请证明;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】我们学过正多边形及其性质,了解了正多边形各边相等、各内角相等、具有轴对称性和旋转不变....下面我们继续探究正五边形相关线段及角的关系:
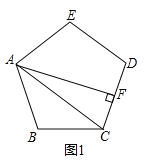
如图1,正五边形![]() 中,
中,
![]() 连接
连接![]() ,并作
,并作![]() ,则
,则![]() 度;
度;
![]() 连接
连接![]() 交
交![]() 于点
于点![]() ,求证:四边形
,求证:四边形![]() 是菱形;
是菱形;
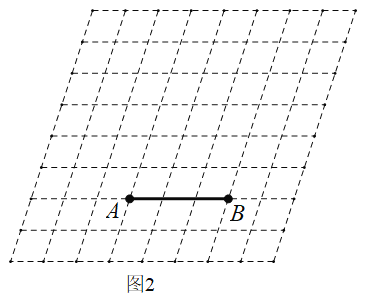
![]() 如图2,是一个斜网格图
如图2,是一个斜网格图![]() , 每个小菱形的较小内角是
, 每个小菱形的较小内角是![]() ,请利用一把角尺(只能画直角和直线,不能度量,可以用三角板替代)在网格图中画出以
,请利用一把角尺(只能画直角和直线,不能度量,可以用三角板替代)在网格图中画出以![]() 为一边的正五边形
为一边的正五边形![]() (保留作图痕迹).
(保留作图痕迹).
查看答案和解析>>
科目: 来源: 题型:
【题目】在新冠状病毒的影响下,某学校积极响应政府号召,开展了“停课不停学”网上授课工作,为了网上授课工作顺利开展和取得良好成效,该校在授课第一周和授课第二周分别随机抽取部分学生进行“网上授课教学效果反馈”网上调查,并将调查结果绘制成如下两幅不完整的统计图,调查显示:两次调查反馈教学效果为“较差”人数相等,第二周反馈教学效果为“很好”人数比例比第一周多![]() ,请根据调查显示和统计图中的信息解决下列问题:
,请根据调查显示和统计图中的信息解决下列问题:
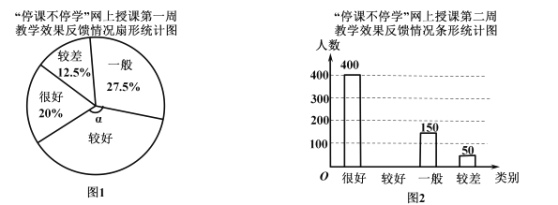
![]() 在图1中,表示“较好”的扇形圆心角
在图1中,表示“较好”的扇形圆心角![]() 的度数为_ 度,并把图2条形统计图补充完整;
的度数为_ 度,并把图2条形统计图补充完整;
![]() 若把调查反馈教学效果“很好”和“较好”作为网上授课成效良好的标准,该校大约有
若把调查反馈教学效果“很好”和“较好”作为网上授课成效良好的标准,该校大约有![]() 名学生,请估计授课第二周学校网上授课成效良好的学生人数;
名学生,请估计授课第二周学校网上授课成效良好的学生人数;
![]() 有一位家长认为,两次调查反馈授课效果为“较差”人数相等,因此学校在一周后调整的措施并没有提高网上授课效果,这位家长分析数据的方法合理吗?请结合统计图,对这位家长分析数据的方法及学校在一周后调整措施对网上授课效果的影响谈谈你的看法.
有一位家长认为,两次调查反馈授课效果为“较差”人数相等,因此学校在一周后调整的措施并没有提高网上授课效果,这位家长分析数据的方法合理吗?请结合统计图,对这位家长分析数据的方法及学校在一周后调整措施对网上授课效果的影响谈谈你的看法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com