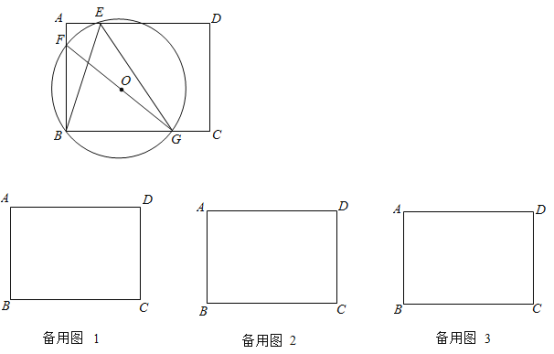
【题目】如图，在矩形中，，，点是边上一点，且，点在边上，过点、、作圆，交边或其延长线于，连接，，，设（）．

（1）求的值；

（2）若，求的值；

（3）若，求弧的长；

（4）若圆经过矩形的两个顶点时，直接写出的值．

（注：，，）

【题目】某超市一段时期内对某种商品经销情况进行统计得到该商品的销售数量（件）由基础销售量与浮动销售量两个部分组成，其中基本销售量保持不变，浮动销售量与售价（元/件，）成反比例，销售过程中得到的部分数据如下：

（1）求与之间的函数关系式；

（2）当该商品销售数量为50件时，求每件商品的售价；

（3）设销售总额为，求的最大值．

【题目】如图，已知，，，交于点，交于点．

（1）求证：；

（2）当时，证明四边形是菱形；

（3）若的外心在其内部，，直接写出的值．

（1）求这五名医护人员的年龄的众数；

（2）若因疫情需要，需增加一名医护人员，若增加后年龄的中位数小于原来年龄的中位数，则增加医护人员的最大年龄是多少？

（3）若需要从男性队员中选两名参加重症病人抢救，求所选两名队员的年龄恰好相等的概率．

【题目】如图，以正六边形的对角线为边，向右作等边三角形，若四边形的面积为4，则五边形的面积为（ ）

A.6B.8C.10D.12

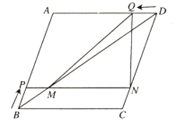
【题目】如图，在菱形ABCD中，AB=5cm，BD=8cm．点P从点B出发，沿BA方向匀速运动，速度为；同时，点Q从点D出发，沿DA方向匀速运动，速度为1cm/s．过点P作PN∥BC分别交BD，CD于点M,N，连接QM，QN．设运动时间为．解答下列问题：

（1）当为何值时，点在线段的垂直平分线上？

（2）设的面积为，求与的函数关系式；

（3）在运动过程中，是否存在某一时刻，使的面积为菱形面积的，若存在，求出的值；若不存在，请说明理由；

（4）是否存在某一时刻，使为等腰三角形？若存在，请直接写出的值；若不存在，请说明理由．

【题目】（问题提出）：有同样大小正方形256个，拼成如图1所示的的一个大的正方形．请问如果用一条直线穿过这个大正方形的话，最多可以穿过多少个小正方形？

（问题探究）：我们先考虑以下简单的情况：一条直线穿越一个正方形的情况．（如图2）

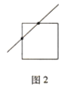
从图中我们可以看出，当一条直线穿过一个小正方形时，这条直线最多与正方形上、下、左、右四条边中的两个边相交，所以当一条直线穿过一个小正方形时，这条直线会与其中某两条边产生两个交点，并且以两个交点为顶点的线段会全部落在小正方形内．

这就启发我们：为了求出直线最多穿过多少个小正方形，我们可以转而去考虑当直线穿越由小正方形拼成的大正方形时最多会产生多少个交点.然后由交点数去确定有多少根小线段，进而通过线段的根数确定下正方形的个数．

再让我们来考虑正方形的情况（如图3）：

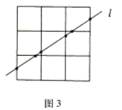
为了让直线穿越更多的小正方形，我们不妨假设直线右上方至左下方穿过一个的正方形，我们从两个方向来分析直线穿过正方形的情况：从上下来看，这条直线由下至上最多可穿过上下平行的两条线段；从左右来看，这条直线最多可穿过左右平行的四条线段；这样直线最多可穿过的大正方形中的六条线段，从而直线上会产生6个交点，这6个交点之间的5条线段，每条会落在一个不同的正方形内，因此直线最多能经过5个小正方形．

（问题解决）：

（1）有同样大小的小正方形16个，拼成如图4所示的的一个大的正方形．如果用一条直线穿过这个大正方形的话，最多可以穿过_________个小正方形．

（2）有同样大小的小正方形256个，拼成的一个大的正方形.如果用一条直线穿过这个大正方形的话，最多可以穿过___________个小正方形．

（3）如果用一条直线穿过的大正方形的话，最多可以穿过___________个小正方形．

（问题拓展）：

（4）如果用一条直线穿过的大长方形的话（如图5），最多可以穿过个___________小正方形．

（5）如果用一条直线穿过的大长方形的话（如图6），最多可以穿过___________个小正方形．

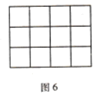
（6）如果用一条直线穿过的大长方形的话，最多可以穿过________个小正方形．

（类比探究）：

由二维的平面我们可以联想到三维的立体空间，平面中的正方形中四条边可联想到正方体中的正方形的六个面，类比上面问题解决的方法解决如下问题：

（7）如图7有同样大小的小正方体8个，拼成如图所示的的一个大的正方体.如果用一条直线穿过这个大正方体的话，最多可以穿过___________个小正方体．

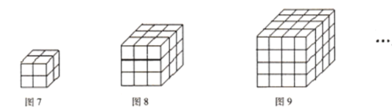
（8）如果用一条直线穿过的大正方体的话，最多可以穿过_________个小正方体．

（1）求出饮料厂每天的利润（元）与批发单价（元）之间的函数关系式；

（2）批发单价定为多少元时，饮料厂每天的利润最大，最大利润是多少元；

（3）如果该饮料厂要使每天的利润不低于18750元，且每天的总成本不超过42500元，那么批发单价应控制在什么范围．（每天的总成本每瓶的成本每天的经销量）

【题目】已知：如图，在四边形ABCD中，AB⊥AC，DC⊥AC，∠B=∠D，，，，点E，F分别是BC，AD的中点．

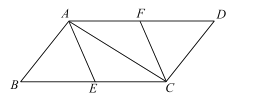
（1）求证：；

（2）当与满足什么数量关系时，四边形是正方形？请证明．

【题目】已知：如图，ABC是等腰直角三角形，∠B=90°，点B的坐标为(1,2)．反比例函数的图象经过点C，一次函数y=ax+b的图象经A,C两点．

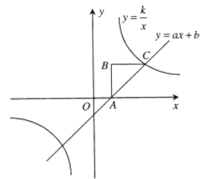
（1）求反比例函数和一次函数的关系式；

（2）直接写出不等式组0<ax+b≤的解集．