
科目: 来源: 题型:
【题目】如图,AB为⊙O的直径,AB=4,C为半圆AB的中点,P为![]() 上一动点,延长BP至点Q,使BPBQ=AB2.若点P由A运动到C,则点Q运动的路径长为_____.
上一动点,延长BP至点Q,使BPBQ=AB2.若点P由A运动到C,则点Q运动的路径长为_____.

查看答案和解析>>
科目: 来源: 题型:
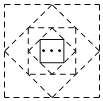
【题目】如图,小聪用一张面积为1的正方形纸片,按如下方式操作:
①将正方形纸片四角向内折叠,使四个顶点重合,展开后沿折痕剪开,把四个等腰直角三角形扔掉;
②在余下纸片上依次重复以上操作,
当完成第2020次操作时,余下纸片的面积为( )
A.22019B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】若点A(﹣1,y1),B(2,y2),C(3,y3)在反比例函数y=![]() (k<0)的图象上.则y1、y2、y3的大小关系是( )
(k<0)的图象上.则y1、y2、y3的大小关系是( )
A.y1>y2>y3B.y3>y2>y1C.y2>y3>y1D.y1>y3>y2
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线与x轴交于A,B两点,与y轴交于点C(0,﹣2),点A的坐标是(2,0),P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E,抛物线的对称轴是直线x=﹣1.
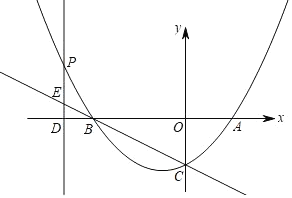
(1)求抛物线的函数表达式;
(2)若点P在第二象限内,且PE=![]() OD,求△PBE的面积.
OD,求△PBE的面积.
(3)在(2)的条件下,若M为直线BC上一点,在x轴的上方,是否存在点M,使△BDM是以BD为腰的等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接DG,过点A作AH∥DG,交BG于点H.连接HF,AF,其中AF交EC于点M.
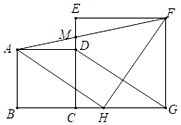
(1)求证:△AHF为等腰直角三角形.
(2)若AB=3,EC=5,求EM的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:有一组邻边相等且对角互补的四边形叫做等补四边形.
理解:
![]() 如图1,点
如图1,点![]() 在
在![]() 上,
上,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,连接
,连接![]() 求证:四边形
求证:四边形![]() 是等补四边形;
是等补四边形;
探究:
![]() 如图2,在等补四边形
如图2,在等补四边形![]() 中
中![]() 连接
连接![]() 是否平分
是否平分![]() 请说明理由.
请说明理由.
运用:
![]() 如图3,在等补四边形
如图3,在等补四边形![]() 中,
中,![]() ,其外角
,其外角![]() 的平分线交
的平分线交![]() 的延长线于点
的延长线于点![]() 求
求![]() 的长.
的长.
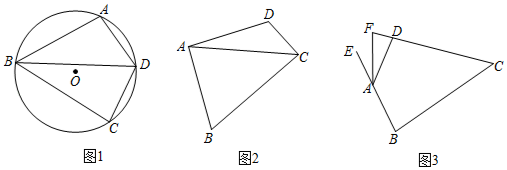
查看答案和解析>>
科目: 来源: 题型:
【题目】为了加快“智慧校园”建设,某市准备为试点学校采购一批![]() 、
、![]() 两种型号的一体机,经过市场调查发现,今年每套
两种型号的一体机,经过市场调查发现,今年每套![]() 型一体机的价格比每套
型一体机的价格比每套![]() 型一体机的价格多0.6万元,且用960万元恰好能购买500套
型一体机的价格多0.6万元,且用960万元恰好能购买500套![]() 型一体机和200套
型一体机和200套![]() 型一体机.
型一体机.
(1)求今年每套![]() 型、
型、![]() 型一体机的价格各是多少万元
型一体机的价格各是多少万元
(2)该市明年计划采购![]() 型、
型、![]() 型一体机1100套,考虑物价因素,预计明年每套
型一体机1100套,考虑物价因素,预计明年每套![]() 型一体机的价格比今年上涨25%,每套
型一体机的价格比今年上涨25%,每套![]() 型一体机的价格不变,若购买
型一体机的价格不变,若购买![]() 型一体机的总费用不低于购买
型一体机的总费用不低于购买![]() 型一体机的总费用,那么该市明年至少需要投入多少万元才能完成采购计划?
型一体机的总费用,那么该市明年至少需要投入多少万元才能完成采购计划?
查看答案和解析>>
科目: 来源: 题型:
【题目】某校开发了“书画、器乐、戏曲、棋类”四大类兴趣课程.为了解全校学生对每类课程的选择情况,随机抽取了若干名学生进行调查(每人必选且只能选一类),先将调查结果绘制成如下两幅不完整的统计图:
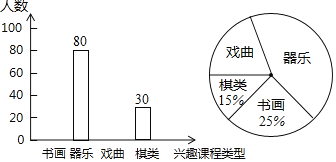
(1)本次随机调查了多少名学生?
(2)补全条形统计图中“书画”、“戏曲”的空缺部分;
(3)若该校共有![]() 名学生,请估计全校学生选择“戏曲”类的人数;
名学生,请估计全校学生选择“戏曲”类的人数;
(4)学校从这四类课程中随机抽取两类参加“全市青少年才艺展示活动”,用树形图或列表法求处恰好抽到“器乐”和“戏曲”类的概率.(书画、器乐、戏曲、棋类可分别用字幕![]() 表示)
表示)
查看答案和解析>>
科目: 来源: 题型:
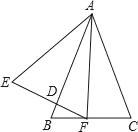
【题目】如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:①∠AFC=∠C;②DF=BF;③△ADE∽△FDB;④∠BFD=∠CAF.其中正确的结论是_____(填写所有正确结论的序号).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() 和点
和点![]() ,顶点为
,顶点为![]() .
.
(1)求![]() 、
、![]() 的值;
的值;
(2)若![]() 的坐标为
的坐标为![]() ,当
,当![]() 时,二次函数
时,二次函数![]() 有最大值
有最大值![]() ,求
,求![]() 的值;
的值;
(3)直线![]() 与直线
与直线![]() 、直线
、直线![]() 分别相交于
分别相交于![]() 、
、![]() ,若抛物线
,若抛物线![]() 与线段
与线段![]() (包含
(包含![]() 、
、![]() 两点)有两个公共点,求
两点)有两个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com