
科目: 来源: 题型:
【题目】疫情突发,危难时刻,从决定建造到交付使用,雷神山、火神山医院仅用时十天,其建造速度之快,充分展现了中国基建的巨大威力!这样的速度和动员能力就是全 国人民的坚定信心和尽快控制疫情的底气!改革开放![]() 年来,中国已经成为领先世界的基 建强国,如图①是建筑工地常见的塔吊,其主体部分的平面示意图如图②,点
年来,中国已经成为领先世界的基 建强国,如图①是建筑工地常见的塔吊,其主体部分的平面示意图如图②,点![]() 在线段
在线段![]() 上运动,
上运动,![]() 垂足为点
垂足为点![]() 的延长线交
的延长线交![]() 于点
于点 ![]() ,经测量
,经测量![]()
![]() ,
,

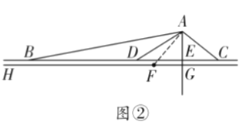
(1)求线段![]() 的长度;(结果 精确到
的长度;(结果 精确到![]() )
)
(2)连接![]() ,当线段
,当线段![]() 时, 求点
时, 求点![]() 和点
和点![]() 之间的距离.(结果 精确到
之间的距离.(结果 精确到![]() ,参考数据:
,参考数据:![]()
![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】列分式方程解应用题:
“5G改变世界,5G创造未来”.2019年9月,全球首个5G上海虹桥火车站,完成了5G网络深度覆盖,旅客可享受到高速便捷的5G网络服务.虹桥火车站中5G网络峰值速率为4G网络峰值速率的10倍.在峰值速率下传输7千兆数据,5G网络比4G网络快630秒,求5G网络的峰值速率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.
(1)利用尺规作出∠DAC的平分线AM,连接BE并延长交AM于点F,(要求在图中标明相应字母,保留作图痕迹,不写作法);
(2)试判断AF与BC有怎样的位置关系与数量关系,并说明理由.
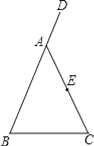
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年9月30日,由著名导演李仁港执导的电影《攀登者》在各大影院上映后,好评不断,小亮和小丽都想去观看这部电影,但是只有一张电影票,于是他们决定采用模球的办法决定胜负,获胜者去看电影,游戏规则如下:在一个不透明的袋子中装有编号1-4的四个球(除编号外都相同),从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字,若两次数字之和大于5,则小亮获胜,若两次数字之和小于5,则小丽获胜.
(1)请用列表或画树状图的方法表示出随机摸球所有可能的结果;
(2)分别求出小亮和小丽获胜的概率,并判断这种游戏规则对两人公平吗?
查看答案和解析>>
科目: 来源: 题型:
【题目】根据某网站调查,2019年网民最关注的热点话题分别是:消费、教育、环保、反腐及其他共五类,根据调查的部分相关数据绘制的统计图如图:
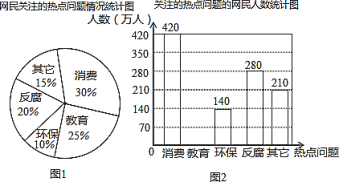
根据以上信息解答下列问题:
(1)请补全条形图,并在图中标明相应数据.
(2)若某市中心城区约有90万人口,请你估计该市中心城区最关注教育问题的人数约有多少万人?
(3)据统计,2017年网民最关注教育问题的人数所占百分比约为10%,则从2017年到2019年关注该问题网民数的年平均增长率约为多少?(已知2017~2019年每年接受调查的网民人数相同,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径![]() .此时圆内接正六边形的周长为
.此时圆内接正六边形的周长为![]() ,如果将圆内接正六边形的周长等同于圆的周长,可得圆周率为3.当正十二边形内接于圆时,如果按照上述方法计算,可得圆周率为______.(参考数据:
,如果将圆内接正六边形的周长等同于圆的周长,可得圆周率为3.当正十二边形内接于圆时,如果按照上述方法计算,可得圆周率为______.(参考数据:![]() )
)
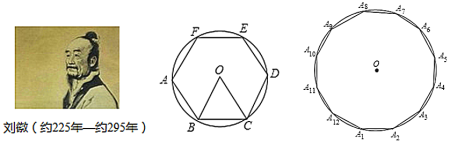
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,甲、乙两同学从![]() 地出发,骑自行车在同一条路上行驶到
地出发,骑自行车在同一条路上行驶到![]() 地,他们离出发地的距离为
地,他们离出发地的距离为![]() 和行驶时间
和行驶时间![]() 之间的函数关系的图像如图所示,则下列结论错误的是( )
之间的函数关系的图像如图所示,则下列结论错误的是( )
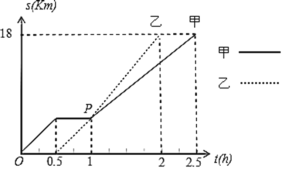
A.![]() 、
、![]() 两地相距
两地相距![]() B.甲在途中停留了0.5小时
B.甲在途中停留了0.5小时
C.全程乙比甲少用了1小时D.乙出发后0.5小时追上甲
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+3与y轴交于点A,与x轴交于点B,抛物线y=﹣
x+3与y轴交于点A,与x轴交于点B,抛物线y=﹣![]() x2+bx+c经过点A和点B,过点A作AC⊥AB交抛物线于点C,过点C作CD⊥y轴于点D,点E在线段AC上,连接ED,且ED=EC,连接EB交y轴于点F.
x2+bx+c经过点A和点B,过点A作AC⊥AB交抛物线于点C,过点C作CD⊥y轴于点D,点E在线段AC上,连接ED,且ED=EC,连接EB交y轴于点F.
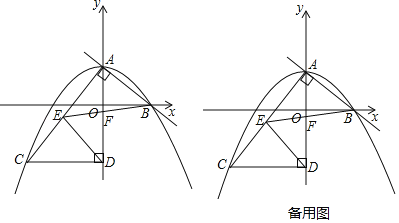
(1)求抛物线的表达式;
(2)求点C的坐标;
(3)若点G在直线AB上,连接FG,当∠AGF=∠AFB时,直接写出线段AG的长;
(4)在(3)的条件下,点H在线段ED上,点P在平面内,当△PAG≌△PDH时,直接写出点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知△ABC是等边三角形,点D为平面内一点,连接DB、DC,∠BDC=120°.
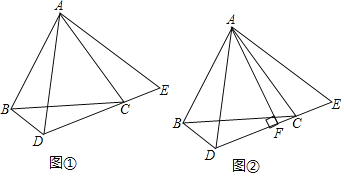
(1)如图①,当点D在BC下方时,连接AD,延长DC到点E,使CE=BD,连接AE.
①求证:△ABD≌△ACE;
②如图②,过点A作AF⊥DE于点F,直接写出线段AF、BD、DC间的数量关系;
(2)若AB=2![]() ,DC=6,直接写出点A到直线BD的距离.
,DC=6,直接写出点A到直线BD的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,ABOC的顶点A(0,2),点B(﹣4,0),点O为坐标原点,点C在第一象限,若将△AOB沿x轴向右运动得到△EFG(点A、O、B分别与点E、F、G对应),运动速度为每秒2个单位长度,边EF交OC于点P,边EG交OA于点Q,设运动时间为t(0<t<2)秒.
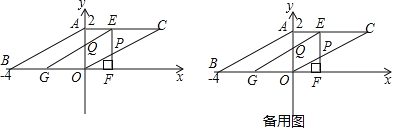
(1)在运动过程中,线段AE的长度为 (直接用含t的代数式表示);
(2)若t=1,求出四边形OPEQ的面积S;
(3)在运动过程中,是否存在四边形OPEQ为菱形?若存在,直接写出此时四边形OPEQ的面积;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com