
科目: 来源: 题型:
【题目】如图,在△ABC和△DCB中,AB = DC,AC = DB,AC与DB交于点M.

【1】求证:△ABC≌△DCB
【2】过点C作CN∥BD,过点B作BN∥AC,CN与BN交于点N,试判断线段BN与CN的数量关系,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的方程mx2+(4-3m)x+2m-8=0(m>0).
(1)求证:方程有两个不相等的实数根;
(2)设方程的两个根分别为x1、x2(x1<x2),若n=x2-x1![]() m,且点B(m,n)在x轴上,求m的值.
m,且点B(m,n)在x轴上,求m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2,正确的个数为

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
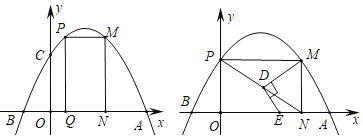
【题目】如图1,抛物线y=ax2+bx+2与x轴交于A,B两点,与y轴交于C点,A(5,0)且AB=3OC,P为x轴上方抛物线上的动点(P不与A,B重合),过点P作PQ⊥x轴于点Q,作PM与x轴平行,交抛物线另一点M,以PQ,PM为邻边作矩形PQNM.
(1)求抛物线的函数表达式;
(2)设矩形PQNM的周长为C,求C的取值范围;
(3)如图2,当P点与C点重合时,连接对角线PN,取PN上一点D(不与P,N重合),连接DM,作DE⊥DM,交x轴于点E.
①试求![]() 的值;
的值;
②试探求是否存在点D,使△DEN是等腰三角形?若存在,请直接写出符合条件的点D坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC和△ADE中,BA=BC,DA=DE,且∠ABC=∠ADE,点E在△ABC的内部,连接EC,EB和ED,设EC=kBD(k≠0).
(1)当∠ABC=∠ADE=60°时,如图1,请求出k值,并给予证明;
(2)当∠ABC=∠ADE=90°时:
①如图2,(1)中的k值是否发生变化,如无变化,请给予证明;如有变化,请求出k值并说明理由;
②如图3,当D,E,C三点共线,且E为DC中点时,请求出tan∠EAC的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,反比例函数![]() (k>0)图象经过等边△OAB的一个顶点B,点A坐标为(2,0),过点B作BM⊥x轴,垂足为M.
(k>0)图象经过等边△OAB的一个顶点B,点A坐标为(2,0),过点B作BM⊥x轴,垂足为M.
(1)求点B的坐标和k的值;
(2)若将△ABM沿直线AB翻折,得到△ABM',判断该反比例函数图象是从点M'的上方经过,还是从点M'的下方经过,又或是恰好经过点M',并说明理由;
(3)如图2,在x轴上取一点A1,以AA1为边长作等边△AA1B1,恰好使点B1落在该反比例函数图象上,连接BB1,求△ABB1的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】今年我区作为全国作文教学改革试验区,举办了中小学生现场作文大赛,全区七、八年级的学生参加了中学组的比赛,大赛组委会对参赛获奖作品的成绩进行统计,每篇获奖作品成绩为m分(60≤m≤100)绘制了如下两幅数据信息不完整的统计图表.
获奖作品成绩频数分布表
分数段 | 频数 | 频率 |
60≤x<70 | 38 | 0.38 |
70≤x<80 | a | 0.32 |
80≤x<90 | b | |
90≤x<100 | 10 | |
合计 | 1 |
请根据以上信息,解决下列问题:
(1)获奖作品成绩频数分布表中a= ,b= ;
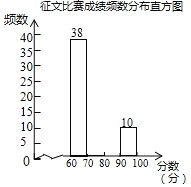
(2)把获奖作品成绩频数分布直方图缺失的信息补全;
(3)某校八年级二班有两名男同学和两名女同学在这次大赛中获奖,并且其中两名同学获得了大赛一等奖,请用列表或画树状图法求出恰好一男一女获得一等奖的概率.
查看答案和解析>>
科目: 来源: 题型:
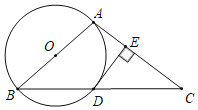
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,过点D作DE⊥AC于点E.
(1)求证:DE是⊙O切线;
(2)若tanB=![]() ,BC=16,求⊙O直径AB的长.
,BC=16,求⊙O直径AB的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为美化校园,计划对面积为400平方米的花坛区域进行绿化,安排甲工程队或乙工程队完成.已知甲队平均每天完成绿化的面积是乙队的2倍,并且甲队比乙队能少用4天完成任务,求甲、乙两工程队平均每天能完成绿化的面积分别是多少平方米?
查看答案和解析>>
科目: 来源: 题型:
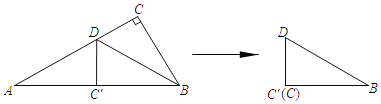
【题目】如图1,小军有一张Rt△ABC纸片,其中∠A=30°,AB=12cm.他先将该纸片沿BD折叠,使点C刚好落在斜边AB上的一点C′处.然后沿DC′剪开得到双层△BDC′(如图2).小军想把双层△BDC′沿某直线再剪开一次,使展开后的两个平面图形中其中一个是平行四边形,则他能得到的平行四边形的最大面积可为____cm2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com