
科目: 来源: 题型:
【题目】由一些大小相等的小正方体组成的几何体的主视图与左视图相同如图所示,设组成这个几何体的小正方体个数最少为m,最多为n,若以m,n的值分别为某个等腰三角形的两条边长,则该等腰三角形的周长为( )

A. 11或13B. 13或14C. 13D. 12或13或14或15
查看答案和解析>>
科目: 来源: 题型:
【题目】某宾馆有单人间、双人间和三人间三种客房供游客租住,某旅行团有18人准备同时租用这三种客房共9间,且每个房间都住满,则租房方案共有( )种.
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目: 来源: 题型:
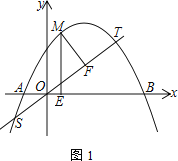
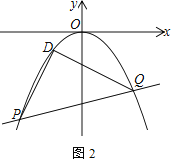
【题目】已知抛物线C:y=ax2-2ax+c经过点C(1,2),与x轴交于A(-1,0)、B两点
(1) 求抛物线C的解析式
(2) 如图1,直线![]() 交抛物线C于S、T两点,M为抛物线C上A、T之间的动点,过M点作ME⊥x轴于点E,MF⊥ST于点F,求ME+MF的最大值
交抛物线C于S、T两点,M为抛物线C上A、T之间的动点,过M点作ME⊥x轴于点E,MF⊥ST于点F,求ME+MF的最大值
(3) 如图2,平移抛物线C的顶点到原点得抛物线C1,直线l:y=kx-2k-4交抛物线C1于P、Q两点,在抛物线C1上存在一个定点D,使∠PDQ=90°,求点D的坐标
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图①,将∠D=60°的菱形ABCD沿对角线AC剪开,将△ADC沿射线DC方向平移,得到△BCE,点M为边BC上一点(点M不与点B、点C重合),将射线AM绕点A逆时针旋转60°,与EB的延长线交于点N,连接MN.
(1)①求证:∠ANB=∠AMC;
②探究△AMN的形状;
(2)如图②,若菱形ABCD变为正方形ABCD,将射线AM绕点A逆时针旋转45°,原题其他条件不变,(1)中的①、②两个结论是否仍然成立?若成立,请直接写出结论;若不成立,请写出变化后的结论并证明.

查看答案和解析>>
科目: 来源: 题型:
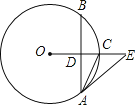
【题目】如图,在⊙O中,半径OC垂直于弦AB,垂足为点D,点E在OC的延长线上,∠EAC=∠BAC
(1)求证:AE是⊙O的切线;
(2)若AB=8,cosE=![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】第36届全国信息学冬令营在广州落下帷幕,长郡师生闪耀各大赛场,金牌数、奖牌数均稳居湖南省第一.学校拟预算7700元全部用于购买甲、乙、丙三种图书共20套奖励获奖师生,其中甲种图书每套500元,乙种图书每套400元,丙种图书每套250元,设购买甲种图书x套,乙种图书y套,请解答下列问题:
(1)请求出y与x的函数关系式(不需要写出自变量的取值范围);
(2)若学校购买的甲、乙两种图书共14套,求甲、乙图书各多少套?
(3)若学校购买的甲、乙两种图书均不少于1套,则有哪几种购买方案?
查看答案和解析>>
科目: 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目: 来源: 题型:
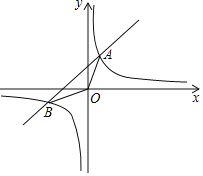
【题目】如图,已知一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象相交于A、B两点,且点A的坐标是(1,2),点B的坐标是(﹣2,w).
(m≠0)的图象相交于A、B两点,且点A的坐标是(1,2),点B的坐标是(﹣2,w).
(1)求一次函数与反比例函数的解析式;
(2)在x轴的正半轴上找一点C,使△AOC的面积等于△ABO的面积,并求出点C的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a,b,c]称为“抛物线系数”.
(1)任意抛物线都有“抛物线三角形”是______(填“真”或“假”)命题;
(2)若一条抛物线系数为[1,0,-2],则其“抛物线三角形”的面积为________;
(3)若一条抛物线系数为[-1,2b,0],其“抛物线三角形”是个直角三角形,求该抛物线的解析式;
(4)在(3)的前提下,该抛物线的顶点为A,与x轴交于O,B两点,在抛物线上是否存在一点P,过P作PQ⊥x轴于点Q,使得△BPQ∽△OAB,如果存在,求出P点坐标,如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com