
科目: 来源: 题型:
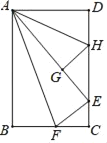
【题目】在数学拓展课《折叠矩形纸片》上,小林折叠矩形纸片ABCD进行如下操作:①把△ABF翻折,点B落在CD边上的点E处,折痕AF交BC边于点F;②把△ADH翻折,点D落在AE边长的点G处,折痕AH交CD边于点H.若AD=6,AB=10,则![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
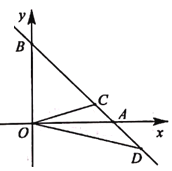
【题目】如图,直线y=-x+2分别交x轴、y轴于点A,B,点D在BA的延长线上,OD的垂直平分线交线段AB于点C.若△OBC和△OAD的周长相等,则OD的长是( )
A. 2B. 2![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目: 来源: 题型:
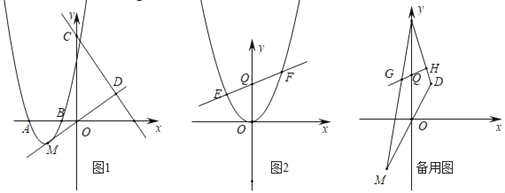
【题目】如图1,抛物线y=ax2+bx+3经过点A(﹣3,0),B(﹣1,0)两点,抛物线的顶点为M,直线y=﹣4x+9与y轴交于点C,与直线OM交于点D.
(1)求抛物线的解析式;
(2)过Q(0,3)作不平行于x轴的直线l
①如图2,将抛物线平移,当顶点至原点时,直线l交抛物线于点E、F,在y轴上存在一点P,使△PEF的内心在y轴上,求点P的坐标;
②直线l交△CMD的边CM、CD于点G、H(G点不与M点重合、H点不与D点重合).S四边形MDHG,S△CGH分别表示四边形MDHG和△CGH的面积,试探究![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】【探索新知】:如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.
(1)一个角的平分线 这个角的“巧分线”;(填“是”或“不是”)
(2)如图2,若∠MPN=α,且射线PQ是∠MPN的“巧分线”,则∠MPQ= ;(用含α的代数式表示出所有可能的结果)
【深入研究】:如图2,若∠MPN=60°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成180°时停止旋转,旋转的时间为t秒.
(3)当t为何值时,射线PM是∠QPN的“巧分线”;
(4)若射线PM同时绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止,请直接写出当射线PQ是∠MPN的“巧分线”时t的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】小雨、小华、小星暑假到某超市参加社会实践活动,在活动中他们参加了某种水果的销售工作,已知该水果的进价为8元/千克.他们通过市场调查发现:当销售单价为10元时,那么每天可售出300千克;销售单价每上涨1元,每天的销售量就减少50千克.
(1)求该超市销售这种水果,每天的销售量y(千克)与销售单价x(元/千克)之间的函数关系式;
(2)一段时间后,发现这种水果每天的销售量均不低于250千克,则此时该超市销售这种水果每天获取的利润w(元)最大是多少?
(3)为响应政府号召,该超市决定在暑假期间每销售1千克这种水果就捐赠a元利润(a≤2.5)给希望工程.公司通过销售记录发现,当销售单价不超过13元时,每天扣除捐赠后的日销售利润随销售单价x(元/千克)的增大而增大,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
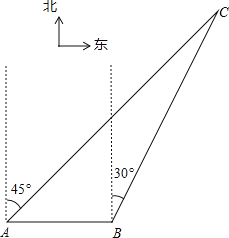
【题目】如图,我渔政310船在南海海面上沿正东方向匀速航行,在A地观测到我渔船C在东北方向上的我国某传统渔场.若渔政310船航向不变,航行半小时后到达B处,此时观测到我渔船C在北偏东30°方向上.问渔政310船再航行多久,离我渔船C的距离最近?(假设我渔船C捕鱼时移动距离忽略不计,结果不取近似值.)
查看答案和解析>>
科目: 来源: 题型:
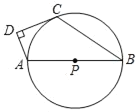
【题目】如图,已知AB是⊙P的直径,点C在⊙P上,D为⊙P外一点,且∠ADC=90°,2∠B+∠DAB=180°.
(1)证明:直线CD为⊙P的切线;
(2)若DC=2![]() ,AD=4,求⊙P的半径.
,AD=4,求⊙P的半径.
查看答案和解析>>
科目: 来源: 题型:
【题目】“足球运球”被列入中招体育必考项目.为此某学校举行“足球运球”达标测试,将成绩10分、9分、8分、7分,对应定为A,B,C,D四个等级.某班根据测试成绩绘制如下统计图,请回答下列问题:
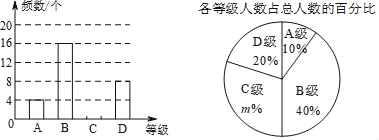
(1)该班级的总人数为 ,m= .
(2)补全条形统计图.
(3)该班“足球运球”测试的平均成绩是多少?
(4)现准备从等级为A的4个人(2男2女)中随机抽取两个人去参加比赛,请用列表或画树状图的方法,求出恰好抽到一男一女的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如果三个数a、b、c满足其中一个数的两倍等于另外两个数的和,我们称这三个数a、b、c是“等差数”若正比例函数y=2x的图象上有三点A(![]() m﹣1,y1)、B(m,y2)、C(2m+1,y3),且这三点的纵坐标y1、y2、y3是“等差数”,则m=_____.
m﹣1,y1)、B(m,y2)、C(2m+1,y3),且这三点的纵坐标y1、y2、y3是“等差数”,则m=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com