
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=12cm,AD=CD=8cm,动点E从点A出发沿AB以每秒1cm的速度向点B运动,动点F从点B出发沿BA以每秒1cm的速度向点A运动,过点E作AB的垂线交折线AD-DC于点G,以EG、EF为邻边作矩形EFHG,设点E、F运动的时间为t(秒),矩形EFHG与四边形ABCD重叠部分的面积为S(cm2).
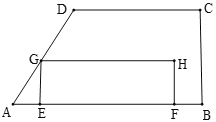
(1)求EG的长(用含t的代数式表示);
(2)当t为何值时,点G与点D重合?
(3)当点G在DC上时,求S(cm2)与t(秒)的函数关系式(S>0);
(4)连接EH、GF、AC、BD,在运动过程中,当这四条线段所在的直线有两条平行时,直接写出t的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校文学社为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
数据收集:从全校随机抽取20名学生,进行了每周用于课外阅读时间的调查,数据如下(单位:min):
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
整理数据:按如下分段整理样本数据并补全表格:
课外阅读时间x(min) | 0≤x<40 | 40≤x<80 | 80≤x<120 | 120≤x<160 |
等级 | D | C | B | A |
人数 | 3 | ____ | 8 | ____ |
分析数据:补全下列表格中的统计量:
平均数 | 中位数 | 众数 |
80 | ____ | ____ |
得出结论:
⑴用样本中的统计量估计该校学生每周用于课外阅读时间的情况等级为_____;
⑵如果该校现有学生400人,估计等级为“B”的学生有多少人?
⑶假设平均阅读一本课外书的时间为320分钟,请你选择样本中的一种统计量估计该校学生每人一年(按52周计算)平均阅读多少本课外书?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是小强洗漱时的侧面示意图,洗漱台(矩形ABCD)靠墙摆放,高AD=80cm,宽AB=48cm,小强身高166cm,下半身FG=100cm.洗漱时下半身与地面成80°角(即∠FGK=80°),身体前倾成125°角(即∠EFG=125°),脚与洗漱台的距离GC=15cm(点D、C、G、K在同一直线上).
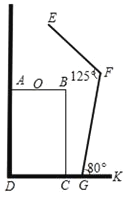
(1)求此时小强头部E点与地面DK的距离;
(2)小强希望他的头部E点恰好在洗漱盆AB的中点O的正上方,他应向前或后退多少(结果精确到0.1cm,参考数据:cos80°≈0.17,sin80°≈0.98,![]() ≈1.41)?
≈1.41)?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在10×10的网格中,有一格点△ABC(说明:顶点都在网格线交点处的三角形叫做格点三角形).
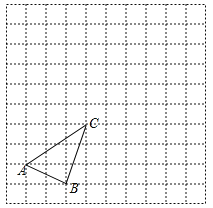
(1)将△ABC先向右平移5个单位,再向上平移2个单位,得到△A'B'C',请直接画出平移后的△A'B'C';
(2)将△A'B'C'绕点C'顺时针旋转90°,得到△A'B'C',请直接画出旋转后的△A'B'C';
(3)在(2)的旋转过程中,求点A'所经过的路线长(结果保留π).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() (x>0)的图象交于A(2,-1)、B(
(x>0)的图象交于A(2,-1)、B(![]() ,n)两点,点C的坐标为(0,2),过点C的直线l与x轴平行.
,n)两点,点C的坐标为(0,2),过点C的直线l与x轴平行.
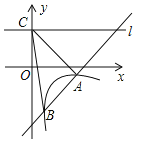
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】九年级(1)班和(2)班分别有一男一女共4名学生报名参加学校文艺汇演主持人的选拔.
(1)若从报名的4名学生中随机选出1名,则所选的这名学生是女生的概率是____;
(2)若从报名的4名学生中随机选出2名,用画树状图或列表的方法写出所有可能的情况,并求出这2名学生来自同一个班级的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7min同时到达C点,甲机器人前3分钟以a m/min的速度行走,乙机器人始终以60m/min的速度行走,如图是甲、乙两机器人之间的距离y(m)与他们的行走时间x(min)之间的函数图象,请结合图象,回答下列问题:
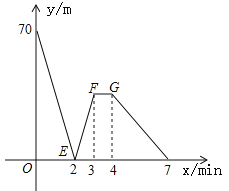
(1)A、B两点之间的距离是____m,A、C两点之间的距离是____m,a=____m/min;
(2)求线段EF所在直线的函数解析式;
(3)设线段FG∥x轴.
①当3≤x≤4时,甲机器人的速度为____m/min;
②直接写出两机器人出发多长时间相距28m.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AD于点E,交BC于点F,连接BE,DF,且BE平分∠ABD.
①求证:四边形BFDE是菱形;
②直接写出∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.

查看答案和解析>>
科目: 来源: 题型:
【题目】某公司购买一批玻璃杯和保温杯,计划用2000元购买玻璃杯,用2800元购买保温杯.已知一个保温杯比一个玻璃杯贵10元.该公司购买的玻璃杯与保温杯的数量能相同吗?
(1)根据题意,甲和乙两同学都先假设该公司购买的玻璃杯与保温杯的数量能相同,并分别列出的方程如下:![]() =
=![]() ;
;![]() -
-![]() =10,根据两位同学所列的方程,请你分别指出未知数x,y表示的意义:x表示 ;y表示 ;
=10,根据两位同学所列的方程,请你分别指出未知数x,y表示的意义:x表示 ;y表示 ;
(2)任选其中一个方程说明该公司购买的玻璃杯与保温杯的数量能否相同.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知A(1,5),直线l1:y=x,直线l2过原点且与x轴正半轴成60°夹角,在l1上有一动点M,在l2上有一动点N,连接AM、MN,则AM+MN的最小值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com