
科目: 来源: 题型:
【题目】如图,点![]() 是线段
是线段![]() 上一点,
上一点,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 的长为半径作⊙
的长为半径作⊙![]() ,过点
,过点![]() 作
作![]() 的垂线交⊙
的垂线交⊙![]() 于
于![]() ,
,![]() 两点,点
两点,点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() 交⊙
交⊙![]() 于点
于点![]() ,以
,以![]() ,
,![]() 为边作
为边作![]() .
.
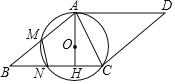
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若![]() ,求四边形
,求四边形![]() 与⊙
与⊙![]() 重叠部分的面积;
重叠部分的面积;
(3)若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 和
和![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C.
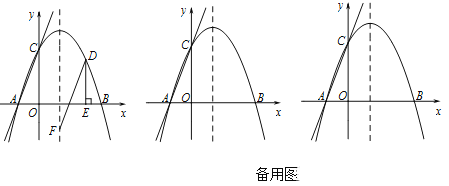
(1)求抛物线y=ax2+2x+c的解析式:;
(2)点D为抛物线上对称轴右侧、x轴上方一点,DE⊥x轴于点E,DF∥AC交抛物线对称轴于点F,求DE+DF的最大值;
(3)①在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;
②点Q在抛物线对称轴上,其纵坐标为t,请直接写出△ACQ为锐角三角形时t的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作FG⊥AC于点F,交AB的延长线于点G.
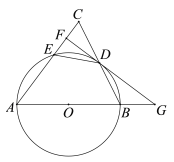
(1)求证:GD为⊙O切线;
(2)求证:DE2=EF·AC;
(3)若tan∠C=2,AB=5,求AE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一次函数![]() ,与反比例函数
,与反比例函数![]() 交于点A(3,1)、B(-1,n),y1交y轴于点C,交x轴于点D.
交于点A(3,1)、B(-1,n),y1交y轴于点C,交x轴于点D.
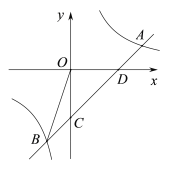
(1)求反比例函数及一次函数的解析式;
(2)求△OBD的面积;
(3)根据图象直接写出![]() >
>![]() 的解集.
的解集.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
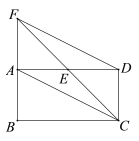
(1)判断四边形ACDF的形状;
(2)当BC=2CD时,求证:CF平分∠BCD.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校创建“环保示范学校”,为了解全校学生参加环保类社团的意愿,在全校随机抽取了50名学生进行问卷调查.问卷给出了五个社团供学生选择(学生可根据自己的爱好选择一个社团,也可以不选),对选择了社团的学生的问卷情况进行了统计,如下表:
社团名称 | A 酵素制作社团 | B 回收材料小制作社团 | C 垃圾分类社团 | D 环保义工社团 | E 绿植养护社团 |
人数 | 10 | 15 | 5 | 10 | 5 |
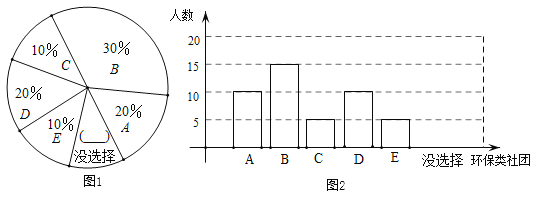
(1)根据以上信息填空:这5个数的中位数是______;扇形图中没选择的百分比为______;
(2)①补全条形统计图;②若该校有1400名学生,根据调查统计情况,请估计全校有多少学生愿意参加环保义工社团;
(3)若小诗和小雨两名同学在酵素制作社团或绿植养护社团中任意选择一个参加,请用树状图或列表法求出这两名同学同时选择绿植养护社团的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在一笔直的海岸线l上有相距2km的A,B两个观测站,B站在A站的正东方向上,从A站测得船C在北偏东60°的方向上,从B站测得船C在北偏东30°的方向上,则船C到海岸线l的距离为多少千米?(参考数据:![]() ≈1.732,结果保留小数点后一位)
≈1.732,结果保留小数点后一位)
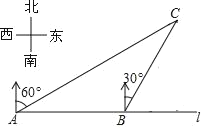
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=2,点E在CD上,DE=1,点F是边AB上一动点,以EF为斜边作Rt△EFP.若点P在矩形ABCD的边上,且这样的直角三角形恰好有两个,则AF的值是________.
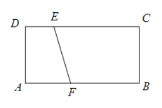
查看答案和解析>>
科目: 来源: 题型:
【题目】某水果店5月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.6月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.
(1)若该店6月份购进这两种水果的数量与5月份都相同,将多支付货款300元,求该店5月份购进甲、乙两种水果分别是多少千克?
(2)若6月份将这两种水果进货总量减少到120千克,且甲种水果不超过乙种水果的3倍,则6月份该店需要支付这两种水果的货款最少应是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】对于二次函数y=ax2-(2a-1)x+a-1(a≠0),有下列结论:①其图象与x轴一定相交;②若a<0,函数在x>1时,y随x的增大而减小;③无论a取何值,抛物线的顶点始终在同一条直线上;④无论a取何值,函数图象都经过同一个点.其中正确结论的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com