
科目: 来源: 题型:
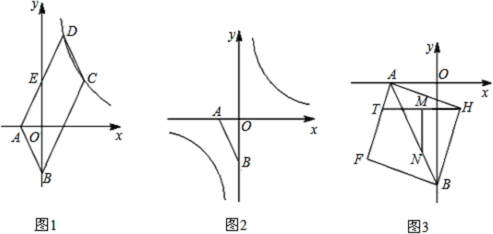
【题目】如图1,已知点![]() ,
,![]() ,且
,且![]() 、
、![]() 满足
满足![]() ,
,![]() 的边
的边![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() 为
为![]() 中点,双曲线
中点,双曲线![]() 经过
经过![]() 、
、![]() 两点.
两点.
(1)求![]() 的值;
的值;
(2)点![]() 在双曲线
在双曲线![]() 上,点
上,点![]() 在
在![]() 轴上,若以点
轴上,若以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,试求满足要求的所有点
为顶点的四边形是平行四边形,试求满足要求的所有点![]() 、
、![]() 的坐标;
的坐标;
(3)以线段![]() 为对角线作正方形
为对角线作正方形![]() (如图
(如图![]() ,点
,点![]() 是边
是边![]() 上一动点,
上一动点,![]() 是
是![]() 的中点,
的中点,![]() ,交
,交![]() 于
于![]() ,当
,当![]() 在
在![]() 上运动时,
上运动时,![]() 的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
查看答案和解析>>
科目: 来源: 题型:
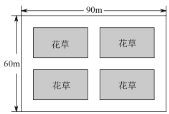
【题目】成都市中心城区“小游园,微绿地”规划已经实施,武侯区某街道有一块矩形空地进入规划试点.如图,已知该矩形空地长为![]() ,宽为
,宽为![]() ,按照规划将预留总面积为
,按照规划将预留总面积为![]() 的四个小矩形区域(阴影部分)种植花草,并在花草周围修建三条横向通道和三条纵向通道,各通道的宽度相等.
的四个小矩形区域(阴影部分)种植花草,并在花草周围修建三条横向通道和三条纵向通道,各通道的宽度相等.
(1)求各通道的宽度;
(2)现有一工程队承接了对这![]() 的区域(阴影部分)进行种植花草的绿化任务,该工程队先按照原计划进行施工,在完成了
的区域(阴影部分)进行种植花草的绿化任务,该工程队先按照原计划进行施工,在完成了![]() 的绿化任务后,将工作效率提高
的绿化任务后,将工作效率提高![]() ,结果提前
,结果提前![]() 天完成任务,求该工程队原计划每天完成多少平方米的绿化任务?
天完成任务,求该工程队原计划每天完成多少平方米的绿化任务?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线![]() 经过正方形
经过正方形![]() 的顶点
的顶点![]() ,先分别过此正方形的顶点
,先分别过此正方形的顶点![]() 、
、![]() 作
作![]() 于点
于点![]() 、
、![]() 于点
于点![]() .然后再以正方形对角线的交点
.然后再以正方形对角线的交点![]() 为端点,引两条相互垂直的射线分别与
为端点,引两条相互垂直的射线分别与![]() ,
,![]() 交于
交于![]() ,
,![]() 两点.若
两点.若![]() ,
,![]() ,则线段
,则线段![]() 长度的最小值是___.
长度的最小值是___.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,已知抛物线y=﹣x2﹣4x+5交x轴于点A、B两点(点A在点B的左侧),交y轴于点C,点D为抛物线的顶点,连接AD.
(1)求直线AD的解析式.
(2)点E(m,0)、F(m+1,0)为x轴上两点,其中(﹣5<m<﹣3.5)EE′、FF′分别平行于y轴,交抛物线于点E′和F′,交AD于点M、N,当ME′+NF′的值最大时,在y轴上找一点R,使得|RE′﹣RF′|值最大,请求出点R的坐标及|RE′﹣RF′|的最大值.
(3)如图2,在抛物线上是否存在点P,使得△PAC是以AC为底边的等腰三角形,若存在,请出点P的坐标及△PAC的面积,若不存在,请说明理由。

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】某商品的进价为每件20元,售价为每件30元,每月可卖出180件.如果该商品的售价每上涨1元,就会少卖出10件,但每件售价不能高于35元,设每件商品的售价上涨x元(x为整数)时,月销售利润为y元.
(1)求y与x之间的函数解析式,并直接写出自变量x的取值范围.
(2)当每件商品的售价定为多少元时,可获得的月利润最大?最大月利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知∠AOB=120°,点A绕点O顺时针旋转后的对应点A1落在射线OB上,点A绕点A1顺时针旋转后的对应点A2落在射线OB上,点A绕点A2顺时针旋转后的对应点A3落在射线OB上,…,连接AA1,AA2,AA3…,依此作法,则∠AAnAn+1等于______度.(用含n的代数式表示,n为正整数)

查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,A点坐标为(3,4),将线段OA绕原点O逆时针旋转90°得到线段OA′,则点A′的坐标是( )
A. (﹣4,3) B. (﹣3,4)
C. (3,﹣4) D. (4,﹣3)
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(0,2),B(p,q)在直线上,抛物线m经过点B、C(p+4,q),且它的顶点N在直线l上.
(1)若B(-2,1),
①请在平面直角坐标系中画出直线l与抛物线m的示意图;
②设抛物线m上的点Q的模坐标为e(-2≤e≤0)过点Q作x轴的垂线,与直线l交于点H.若QH=d,当d随e的增大面增大时,求e的取值范围;
(2)抛物线m与y轴交于点F,当抛物线m与x轴有唯一交点时,判断△NOF的形状并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com